题目内容
13.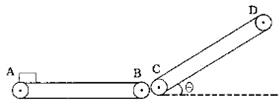 淮北水泥厂采用如图所水的装置来传送水泥,它由两台皮带传送机组成,一台水平传送,A、B两端相距x1=3.5m.另一台倾斜,传送带与地面的倾角θ=37°,C、D两端相距x2=4.45m,B、C相距很近.水平部分AB以v=5m/s的速率顺时针转动.将一袋水泥放在A端,到达B端后,速度大小不变地传到C端,水泥与两传送带间的动摩擦因数均相同.已知水泥袋从A端传到B端的时间为t=1.2s.(取g=10m/s2,sin37°=0.6,cos37°=0.8,)试求:
淮北水泥厂采用如图所水的装置来传送水泥,它由两台皮带传送机组成,一台水平传送,A、B两端相距x1=3.5m.另一台倾斜,传送带与地面的倾角θ=37°,C、D两端相距x2=4.45m,B、C相距很近.水平部分AB以v=5m/s的速率顺时针转动.将一袋水泥放在A端,到达B端后,速度大小不变地传到C端,水泥与两传送带间的动摩擦因数均相同.已知水泥袋从A端传到B端的时间为t=1.2s.(取g=10m/s2,sin37°=0.6,cos37°=0.8,)试求:(1)水泥袋与传送带之间的动摩擦因数μ;
(2)若要水泥袋能被送到D端,求倾斜传送带顺时针运转的最小速度及倾斜传送带在此速度运行下水泥袋从C端到D端所用时间.
分析 (1)水泥放上传送带先做匀加速直线运动,求出水泥达到传送带速度所需的时间和位移,判断水泥在AB段的运动情况,求出匀加速运动的加速度,再由牛顿第二定律求得动摩擦因数μ;
(2)根据水泥传到C端时的速度与传送带速度的关系,分析水泥的运动情况,从而根据运动学规律求出米袋沿传送带从A运动到B的时间.
解答 解:(1)如果水泥袋在AB段一直加速,设其到达B点时的速度为vx.
则有 x1=$\frac{{v}_{x}}{2}t$
解得 vx=5.8m/s>v
说明水泥袋在AB段先匀加速后匀速,设匀加速时间为t1,位移为x1′,匀速时间为t2,位移为x2′.
水泥袋在AB上加速时加速度为a1,则有 μmg=ma1
加速过程有 x1′=$\frac{1}{2}{a}_{1}{t}_{1}^{2}$
v=a1t1
匀速过程有 x2′=vt2;
又因为 x1=x1′+x2′,t=t1+t2
联立解得 μ=0.5
(2)设在CD传送速度为vC时水泥恰能到达D点,水泥袋在CD传送带上速度大于vC时做加速度为 a3=gsinθ+μgcosθ=10m/s2的匀减速运动
位移 x3=$\frac{{v}_{B}^{2}-{v}_{C}^{2}}{2{a}_{3}}$
速度小于vC后做加速度为 a4=gsinθ-μgcosθ=2m/s2的匀减速运动,直到速度减为零,位移 x4=$\frac{{v}_{C}^{2}}{2{a}_{4}}$
又 x3+x4=4.45m
解得 vC=4m/s
水泥袋能被送到D点,则CD部分顺时针运转的最小速度为4m/s.
如果传送带以此速度运行,水泥袋第一阶段减速时间 t3=$\frac{{v}_{B}-{v}_{C}}{{a}_{3}}$
第二阶段减速时间 t4=$\frac{{v}_{C}}{{a}_{4}}$
则水泥袋从C端到D点所用时间 t′=t3+t4=2.1s
答:(1)水泥袋与传送带之间的动摩擦因数μ是0.5.
(2)倾斜传送带顺时针运转的最小速度是4m/s,倾斜传送带在此速度运行下水泥袋从C端到D端所用时间是2.1s.
点评 本题是个多过程问题,关键要理清各个阶段的运动情况,结合牛顿运动定律和运动学研究物体的运动情况.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案 如图所示,虚线a、b、c代表电场中一簇等势线,相邻等势面之间的电势差相等,实线为一带电质点(重力不计)仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中一簇等势线,相邻等势面之间的电势差相等,实线为一带电质点(重力不计)仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )| A. | a、b、c三个等势面中,a的电势最高 | |
| B. | 电场中Q点处的电场强度大小比P点处大 | |
| C. | 该带电质点在P点处受到的电场力比在Q点处大 | |
| D. | 该带电质点在P点具有的电势能比在Q点具有的电势能大 |
| 名称 | 车身 质量 | 满载 载重 | 前后车轮直径 | 额定 转速 | 电动机额定电压 | 电动机额定电流 | 额定机械输出功率 |
| 参数 | 40kg | 80kg | 40cm | $\frac{4500}{2π}$r/min | 48V | 20A | 835W |
(1)电动自行车以额定转速行进时的速度v0;在额定工作状态时,损失的功率有80%是由于电动机绕线电阻生热而产生的,则电动机的绕线电阻为多大;
(2)满载情况下,该车以速度v=5m/s沿着坡度为θ=4.59°的长直坡道向上匀速行驶时,受到的摩擦阻力为车重(含载重)重量的0.02倍,求此状态下电动自行车实际运行机械功率(sin 4.59°=0.08;重力加速度g=10 m/s2).
 如图所示为甲乙两质点作直线运动的速度一时间图象.则下列说法中正确的是( )
如图所示为甲乙两质点作直线运动的速度一时间图象.则下列说法中正确的是( )| A. | 在0~t3时间内甲、乙两质点的平均速度相等 | |
| B. | 甲质点在0~t1时间内的加速度与乙质点在t2~t3时间的加速度相同 | |
| C. | 甲质点在0~t1时间内的平均速度小于乙质点在0~t2时间内平均速度 | |
| D. | 在t3时刻,甲、乙两质点都回到了出发点 |
 如图所示,在投球游戏中,游戏者将小球从P点以速度v0水平抛向固定在水平地面上的筐子,小球恰好砸在筐子的左边外缘而没有进入筐内,若要把小球投入筐内,下列做法可行的是( )
如图所示,在投球游戏中,游戏者将小球从P点以速度v0水平抛向固定在水平地面上的筐子,小球恰好砸在筐子的左边外缘而没有进入筐内,若要把小球投入筐内,下列做法可行的是( )| A. | 在P点以略大于v0的速度将小球水平抛出 | |
| B. | 在P点以略小于v0的速度将小球水平抛出 | |
| C. | 在P点正下方某位置将小球以v0的速度水平抛出 | |
| D. | 在P点左侧与P点等高的某位置将小球以v0的速度水平抛出 |
 如图所示,半圆槽光滑、绝缘、固定,圆心是O,最低点是P,直径MN水平,a、b是两个完全相同的带正电小球(视为点电荷),b固定在M点,a从N点静止释放,沿半圆槽运动经过P点到达某点Q(图中未画出)时速度为零.则小球a( )
如图所示,半圆槽光滑、绝缘、固定,圆心是O,最低点是P,直径MN水平,a、b是两个完全相同的带正电小球(视为点电荷),b固定在M点,a从N点静止释放,沿半圆槽运动经过P点到达某点Q(图中未画出)时速度为零.则小球a( )| A. | 从N到Q的过程中,重力与库仑力的合力先增大后减小 | |
| B. | 从N到P的过程中,速率先增大后减小 | |
| C. | 从N到Q的过程中,电势能先增加后减小 | |
| D. | 从P到Q的过程中,动能减少量小于电势能增加量 |
| A. | α粒子先受到原子核的斥力作用,后受原子核的引力的作用 | |
| B. | α粒子一直受到原子核的斥力作用 | |
| C. | α粒子先受到原子核的引力作用,后受到原子核的斥力作用 | |
| D. | α粒子一直受到库仑斥力,速度一直减小 |
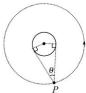 如图所示,飞行器P绕某星球做匀速圆周运动周期为T,已知星球相对飞行器的张角为θ,引力常量为G.求该星球的密度?
如图所示,飞行器P绕某星球做匀速圆周运动周期为T,已知星球相对飞行器的张角为θ,引力常量为G.求该星球的密度?
