题目内容
一个质量为1kg的物体,t=0时初速度为零,在2N的合力作用下沿x轴正方向运动,1s后再增加一个大小也为2N、方向沿y轴正方向的力,则该物体在2s末的速度大小为
4.47
4.47
m/s,前2s内的位移为4.12
4.12
m.分析:先根据牛顿第二定律求解出x、y方向的加速度,根据运动的独立性,分别在x方向和y方向上求解速度和位移,再用勾股定理合成速度和位移,即为实际的要求的速度和位移.
解答:解:根据牛顿第二定律F合=ma,可知
沿x正方向的加速度ax=
=
m/s2=2m/s2
沿y正方向的加速度ay=
=
m/s2=2m/s2
1s末的速度v1=axt1=2×1m/s=2m/s
前1s内的位移x1=
axt12=
×2×12m=1m
接下来,在x方向和y方向都要做匀加速运动,根据运动的独立性,分别求解在这两个方向上的速度和位移,再用勾股定理合成速度和位移.
第2s末,x方向上的速度vx=v1+axt2=2+2×1m/s=4m/s
y方向上的速度vy=ayt2=2×1m/s=2m/s
所以第2s末的实际速度为v=
=
m/s=
m/s≈4.47m/s
第2s内,x方向上发生的位移sx=v1t2+
axt22=2×1+
×2×12m=3m
y方向上发生的位移sy=
ayt22=
×2×12m=1m
前2s内,x方向上发生的总位移x=x1+sx=1+3m=4m
y方向上发生的位移y=sy=
ayt22=1m
所以,前2s内发生的实际位移为s=
=
m=
m≈4.12m
故答案为:4.47,4.12.
沿x正方向的加速度ax=
| Fx |
| m |
| 2 |
| 1 |
沿y正方向的加速度ay=
| Fy |
| m |
| 2 |
| 1 |
1s末的速度v1=axt1=2×1m/s=2m/s
前1s内的位移x1=
| 1 |
| 2 |
| 1 |
| 2 |
接下来,在x方向和y方向都要做匀加速运动,根据运动的独立性,分别求解在这两个方向上的速度和位移,再用勾股定理合成速度和位移.
第2s末,x方向上的速度vx=v1+axt2=2+2×1m/s=4m/s
y方向上的速度vy=ayt2=2×1m/s=2m/s
所以第2s末的实际速度为v=
| vx2+vy2 |
| 42+22 |
| 20 |
第2s内,x方向上发生的位移sx=v1t2+
| 1 |
| 2 |
| 1 |
| 2 |
y方向上发生的位移sy=
| 1 |
| 2 |
| 1 |
| 2 |
前2s内,x方向上发生的总位移x=x1+sx=1+3m=4m
y方向上发生的位移y=sy=
| 1 |
| 2 |
所以,前2s内发生的实际位移为s=
| x2+y2 |
| 42+12 |
| 17 |
故答案为:4.47,4.12.
点评:对于运动的合成与分析问题,主要是考查速度和位移的合成和分解,一定要作好矢量的分解、合成图,根据运动的独立性和等时性求解.

练习册系列答案
相关题目
 如图所示,底板光滑的小车上用两个量程为20N、完全相同的弹簧秤甲和乙系住一个质量为1kg的物块,在水平地面上,当小车做匀速直线运动时,两弹簧秤的示数均为10N.当小车做匀加速直线运动时,弹簧秤甲的示数变为8N,这时小车运动的加速度大小是( )
如图所示,底板光滑的小车上用两个量程为20N、完全相同的弹簧秤甲和乙系住一个质量为1kg的物块,在水平地面上,当小车做匀速直线运动时,两弹簧秤的示数均为10N.当小车做匀加速直线运动时,弹簧秤甲的示数变为8N,这时小车运动的加速度大小是( ) (2011?太原模拟)竖直放置的轻弹簧上,上端与质量为3kg的物块B相连接.另一个质量为1kg的物块A放在B上.先向下压A,然后释放,A、B共同向上运动一段后将分离,分离后A又上升了0.2m到达最高点,此时B的速度方向向下,且弹簧恰好为原长.则从A、B分离到A上升到最高点的过程中,弹簧弹力对B做的功及弹簧回到原长时B的速度大小分别是(g=10m/s2)( )
(2011?太原模拟)竖直放置的轻弹簧上,上端与质量为3kg的物块B相连接.另一个质量为1kg的物块A放在B上.先向下压A,然后释放,A、B共同向上运动一段后将分离,分离后A又上升了0.2m到达最高点,此时B的速度方向向下,且弹簧恰好为原长.则从A、B分离到A上升到最高点的过程中,弹簧弹力对B做的功及弹簧回到原长时B的速度大小分别是(g=10m/s2)( )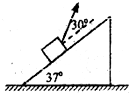 将一个质量为1kg的物块置于倾角为37°的固定斜面上,物块在与斜面夹角为30°的拉力F作用下加速上升,已知物块与斜面间的动摩擦因数为0.2,F大小为10N,则物块上升的加速度约为:(sin37°=0.6,cos37°=0.8,sin30°=0.5,cos30°=0.866)( )
将一个质量为1kg的物块置于倾角为37°的固定斜面上,物块在与斜面夹角为30°的拉力F作用下加速上升,已知物块与斜面间的动摩擦因数为0.2,F大小为10N,则物块上升的加速度约为:(sin37°=0.6,cos37°=0.8,sin30°=0.5,cos30°=0.866)( )

 B.
B.
 D.
D.