题目内容
一个质量为m、直径为d、电阻为R的金属圆环，在范围足够大的磁场中竖直向下下落，磁场的分布情况如图所示．已知磁感强度竖直方向分量By的大小只随高度y变化，其随高度y变化关系为By=B（1+ky）（此处k为比例常数，且k＞0），其中沿圆环轴线的磁场方向始终向上．金属圆环在下落过程中的环面始终保持水平，速度越来越大，最终稳定为某一数值，称为收尾速度．求（1）圆环中感应电流的方向．
（2）圆环收尾速度的大小．
【答案】分析：（1）根据楞次定律判断圆环中的感应电流方向．
（2）当圆环所受的重力与安培力相等时，达到收尾速度．根据法拉第电磁感应定律、结合能量守恒定律求出收尾的速度大小
解答：解：（1）愣次定律可知，感应电流的方向为顺时针（俯视）．
（2）圆环下落高度为y时的磁通量为：
Φ=BS=Bπ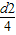
=B（1+ky） π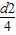
设收尾速度为vm，以vm运动△t时间内磁通量的变化为
△Φ=△BS=Bk△yπ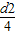
=Bkπ
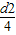vm△t
由法拉第电磁感应定律 ε=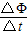
=Bk π 
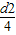vm
圆环中感应电流的电功率为 Pε=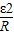
重力做功的功率为 PG=mgvm
能量守恒 Pε=PG
解得 vm=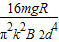
答：
（1）圆环中感应电流的方向为顺时针（俯视）．
（2）圆环收尾速度的大小是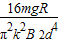
．
点评：解决本题的关键掌握楞次定律判断感应电流的方向，以及掌握法拉第电磁感应定律，能够结合能量守恒定律求出收尾速度．
（2）当圆环所受的重力与安培力相等时，达到收尾速度．根据法拉第电磁感应定律、结合能量守恒定律求出收尾的速度大小
解答：解：（1）愣次定律可知，感应电流的方向为顺时针（俯视）．
（2）圆环下落高度为y时的磁通量为：
Φ=BS=Bπ
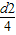=B（1+ky） π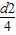 设收尾速度为vm，以vm运动△t时间内磁通量的变化为
△Φ=△BS=Bk△yπ
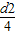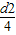=Bkπvm△t 由法拉第电磁感应定律 ε=
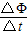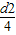=Bk π vm圆环中感应电流的电功率为 Pε=
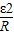
重力做功的功率为 PG=mgvm
能量守恒 Pε=PG
解得 vm=
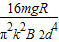
答：
（1）圆环中感应电流的方向为顺时针（俯视）．
（2）圆环收尾速度的大小是
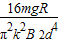．点评：解决本题的关键掌握楞次定律判断感应电流的方向，以及掌握法拉第电磁感应定律，能够结合能量守恒定律求出收尾速度．
练习册系列答案
教材全解字词句篇系列答案
相关题目
（2007?深圳二模）一个质量为m、直径为d、电阻为R的金属圆环，在范围足够大的磁场中竖直向下下落，磁场的分布情况如图所示．已知磁感强度竖直方向分量By的大小只随高度y变化，其随高度y变化关系为By=B0（1+ky）（此处k为比例常数，且k＞0），其中沿圆环轴线的磁场方向始终向上．金属圆环在下落过程中的环面始终保持水平，速度越来越大，最终稳定为某一数值，称为收尾速度．求
一个质量为m、直径为d、电阻为R的金属圆环，在范围很大的磁场中沿竖直方向下落，磁场的分布情况如图所示，已知磁感应强度竖直方向的分量By的大小只随高度变化，其随高度y变化关系为By=B0（1+ky）（此处k为比例常数，且k＞0），其中沿圆环轴线的磁场方向始终竖直向上，在下落过程中金属圆环所在的平面始终保持水平，速度越来越大，最终稳定为某一数值，称为收尾速度．俯视观察，圆环中的感应电流方向为
