题目内容
如图所示，光滑水平面AB与竖直面的半圆形导轨在B点衔接，导轨半径R，一个质量为m的静止物块在A处压缩弹簧，把物块释放，在弹力的作用下获得一个向右的速度，当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍，之后向上运动恰能完成半圆周运动到达C点，求：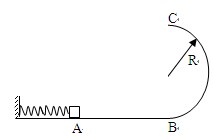
（1）弹簧对物块的弹力做的功；
（2）物块从B至C克服阻力所做的功；
（3）物块离开C点后落回水平面时动能的大小.
【答案】
（1）
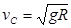（2）
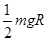（3）
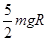
【解析】
试题分析：(1)在B点对物块有: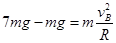
解得：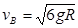
由功能关系有：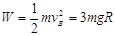 
（2）在C点对物块有：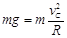 
解得：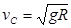
在由B到C过程由功能关系有：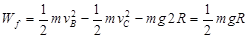 
（3）在由C到落回地面的过程由机械能守恒有：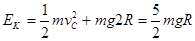 
考点：动能定理的应用；牛顿第二定律；平抛运动；
点评：解答本题首先应明确物体运动的三个过程，第一过程弹力做功增加了物体的动能；第二过程做竖直面上的圆周运动，要注意临界条件的应用；第三过程做平抛运动，机械能守恒．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
如图所示，光滑水平面AB与竖直面内的半圆形导轨在B点相接，导轨半径为R．一个质量为m的物体将弹簧压缩至A点后由静止释放，在弹力作用下物体获得某一向右速度后脱离弹簧，脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍，之后向上运动完成半个圆周运动恰好到达C点．试求：
如图所示，光滑水平面与一半径为R处在竖平面内的光滑圆轨道相切，质量为m的小球（可视为质点）以初速度v0向右运动进入圆轨道，在图中虚线位置脱离轨道，重力加速度为g，下述说法正确的是（ ）
（2013?如东县模拟）如图所示，光滑水平面AB与竖直面内粗糙的半圆形导轨在B点衔接，BC为导轨的直径，与水平面垂直，导轨半径为R，一个质量为m的小球将弹簧压缩至A处．小球从A处由静止释放被弹开后，以速度v经过B点进入半圆形轨道，之后向上运动恰能沿轨道运动到C点，求：
如图所示，光滑水平面内，一根细绳一端固定，另一端系一小球，现让小球在水平面内做匀速圆周运动，则（ ）