题目内容
 如图,在xOy平面的第一、四象限内存在着方向垂直纸面向外、磁感应强度为B的匀强磁场,第四象限内存在方向沿-y方向、电场强度为E的匀强电场。从y轴上坐标为a的一点向磁场区发射速度大小不等的带正电同种粒子,速度方向范围是与+y方向成30º-150º,且在xOy平面内。结果所有粒子经过磁场偏转后都垂直打到x轴上,然后进入第四象限的匀强电场区。已知带电粒子电量为+q,质量为m,重力不计。
如图,在xOy平面的第一、四象限内存在着方向垂直纸面向外、磁感应强度为B的匀强磁场,第四象限内存在方向沿-y方向、电场强度为E的匀强电场。从y轴上坐标为a的一点向磁场区发射速度大小不等的带正电同种粒子,速度方向范围是与+y方向成30º-150º,且在xOy平面内。结果所有粒子经过磁场偏转后都垂直打到x轴上,然后进入第四象限的匀强电场区。已知带电粒子电量为+q,质量为m,重力不计。
(1)确定进入磁场速度最小粒子的速度方向,并求出速度大小。
(2)所有通过磁场区的粒子中,求出最短时间与最长时间的比值。
(3)从x轴上x=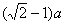 点射入第四象限的粒子穿过电磁场后经过y轴上y=-b的点,求该粒子经过y=-b点的速度大小。
点射入第四象限的粒子穿过电磁场后经过y轴上y=-b的点,求该粒子经过y=-b点的速度大小。
【答案】
(1)设速度v粒子与y轴夹角θ,垂直达到x轴上满足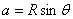 (1分)
(1分)
又
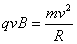 (1分)
(1分) 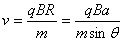 (1分)
(1分)
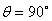 时
时 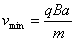 (2分)
(2分)
(2)最长时间对应粒子初速度与y轴正方向夹角30º ,转过150 º
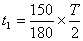 (2分)
(2分)
最短时间对应粒子初速度与y轴负方向夹角30º ,转过30º
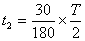 (2分)
(2分)
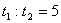 (1分)
(1分)
(3)粒子射出时与y轴负方向夹角θ,则有 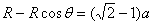 (1分)
(1分)
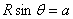 (1分)
(1分)
得到: 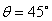
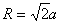 (1分)
(1分)
速度v0为
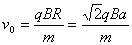 (1分)
(1分)
到达y轴速度v,则
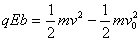 (1分)
(1分)
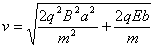 (1分)
(1分)

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
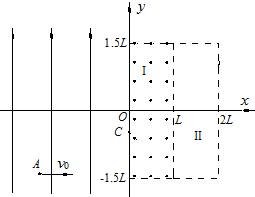 如图所示,在xOy平面的y轴左侧存在沿y轴正方向的匀强电场,y轴右侧区域Ⅰ内存在磁感应强度大小B1=
如图所示,在xOy平面的y轴左侧存在沿y轴正方向的匀强电场,y轴右侧区域Ⅰ内存在磁感应强度大小B1= (2013?常德模拟)如图所示,在xOy平面的第I象限内存在沿y轴负方向的匀强电场,电场强度大小为E;第Ⅱ象限内有半径为R的圆分别与x轴、y轴相切于P、Q 两点,圆内存在垂直于xOy平面向外的匀强磁场.一带正电的粒子(重力不计)以速率v0从P点射入磁场后恰好垂直y轴进入电场,最后从M(
(2013?常德模拟)如图所示,在xOy平面的第I象限内存在沿y轴负方向的匀强电场,电场强度大小为E;第Ⅱ象限内有半径为R的圆分别与x轴、y轴相切于P、Q 两点,圆内存在垂直于xOy平面向外的匀强磁场.一带正电的粒子(重力不计)以速率v0从P点射入磁场后恰好垂直y轴进入电场,最后从M( L)的A点以速度v0沿 +x方向射出,恰好经过坐标为[0,-(
L)的A点以速度v0沿 +x方向射出,恰好经过坐标为[0,-( –1)L]的C点射入区域Ⅰ。粒子重力忽略不计。
–1)L]的C点射入区域Ⅰ。粒子重力忽略不计。
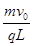 、方向垂直纸面向外的匀强磁场,区域Ⅰ、区域Ⅱ的宽度均为L,高度均为3L。质量为m、电荷量为 +q的带电粒子从坐标为(– 2L,–
、方向垂直纸面向外的匀强磁场,区域Ⅰ、区域Ⅱ的宽度均为L,高度均为3L。质量为m、电荷量为 +q的带电粒子从坐标为(– 2L,– L)的A点以速度v0沿+x方向射出,恰好经过坐标为[0,-(
L)的A点以速度v0沿+x方向射出,恰好经过坐标为[0,-(
 L)的A点以速度v0沿 +x方向射出,恰好经过坐标为[0,-(
L)的A点以速度v0沿 +x方向射出,恰好经过坐标为[0,-( –1)L]的C点射入区域Ⅰ。粒子重力忽略不计。
–1)L]的C点射入区域Ⅰ。粒子重力忽略不计。