题目内容
（2013?常德模拟）如图所示，在xOy平面的第I象限内存在沿y轴负方向的匀强电场，电场强度大小为E；第Ⅱ象限内有半径为R的圆分别与x轴、y轴相切于P、Q 两点，圆内存在垂直于xOy平面向外的匀强磁场．一带正电的粒子（重力不计）以速率v0从P点射入磁场后恰好垂直y轴进入电场，最后从M（| 3 |
（1）带电粒子的比荷；
（2）磁感应强度的大小B；
（3）粒子从射入磁场到射出电场的时间．
分析：（1）粒子垂直于电场进入第一象限，粒子做类平抛运动，由到达M的速度方向可利用速度的合成与分解得知该点y方向的速度．结合牛顿第二定律求得粒子的比荷；
（2）根据运动学的公式，求出粒子进入电场时的位置，画出粒子运动的轨迹，根据图象中的几何关系求出粒子运动的半径，根据半径公式R=
求出磁感应强度；
（3）粒子在洛伦兹力的作用下做匀速圆周运动，利用洛伦兹力提供向心力的公式，求出在磁场中运动的时间．利用平抛运动的规律求出粒子在电场中运动的时间．总时间是各段时间的和．
（2）根据运动学的公式，求出粒子进入电场时的位置，画出粒子运动的轨迹，根据图象中的几何关系求出粒子运动的半径，根据半径公式R=
| mv |
| qB |
（3）粒子在洛伦兹力的作用下做匀速圆周运动，利用洛伦兹力提供向心力的公式，求出在磁场中运动的时间．利用平抛运动的规律求出粒子在电场中运动的时间．总时间是各段时间的和．
解答：解：（1）粒子垂直于电场进入第一象限，粒子做类平抛运动，设粒子在电场中运动的时间为t3，在x方向上：
R=v0t3，得：t3=
y方向：vy=at3=
?t3，
又由于：
=tanα=
联立以上3个公式解得：
=
（2）沿电场线方向粒子的位移：y=
a
=
?
?
=
?
?E?
=
所以粒子进入电场时的坐标N（0，
），所以画出粒子运动的轨迹如图：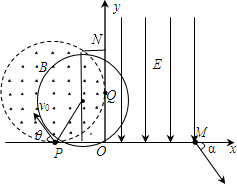
设粒子做圆周运动的半径为r，则r+rcosθ=
，rsinθ=
解以上两个方程得：r=
R
洛伦兹力提供粒子做圆周运动的向心力，得：qv0B=
所以：B=
=
?v0?
=
（3）粒子在磁场中运动的周期：T=
=
设粒子在磁场中运动的时间为t1，在磁场和电场之间运动的时间为t2，
=
，β=π-arcsin
=π-arcsin
=180°-37°=153°
所以：t1=
?
=
粒子在磁场和电场之间运动的时间：t2=
=
粒子从射入磁场到射出电场的时间：t=t1+t2+t3=
+
+
答：（1）带电粒子的比荷
=
；
（2）磁感应强度的大小B=
；
（3）粒子从射入磁场到射出电场的时间t=
+
+
．
| 3 |
| ||
| v0 |
y方向：vy=at3=
| qE |
| m |
又由于：
| vy |
| v0 |
| 3 |
联立以上3个公式解得：
| q |
| m |
| ||
| ER |
（2）沿电场线方向粒子的位移：y=
| 1 |
| 2 |
| t | 2 3 |
| 1 |
| 2 |
| qE |
| m |
| t | 2 3 |
| 1 |
| 2 |
| ||
| ER |
| 3R2 | ||
|
| 3R |
| 2 |
所以粒子进入电场时的坐标N（0，
| 3R |
| 2 |
设粒子做圆周运动的半径为r，则r+rcosθ=
| 3R |
| 2 |
| R |
| 2 |
解以上两个方程得：r=
| 5 |
| 6 |
洛伦兹力提供粒子做圆周运动的向心力，得：qv0B=
m
| ||
| r |
所以：B=
| mv0 |
| qr |
| ER | ||
|
| 5 |
| 6R |
| 5E |
| 6v0 |
（3）粒子在磁场中运动的周期：T=
| 2πr |
| v0 |
| 5πR |
| 3v0 |
设粒子在磁场中运动的时间为t1，在磁场和电场之间运动的时间为t2，
| t1 |
| T |
| β |
| 360° |
| ||
| r |
| 3 |
| 5 |
所以：t1=
| 153° |
| 360° |
| 5πR |
| 3v0 |
| 17πR |
| 24v0 |
粒子在磁场和电场之间运动的时间：t2=
| ||
| v0 |
| R |
| 2v0 |
粒子从射入磁场到射出电场的时间：t=t1+t2+t3=
| 17πR |
| 24v0 |
| R |
| 2v0 |
| ||
| v0 |
答：（1）带电粒子的比荷
| q |
| m |
| ||
| ER |
（2）磁感应强度的大小B=
| 5E |
| 6v0 |
（3）粒子从射入磁场到射出电场的时间t=
| 17πR |
| 24v0 |
| R |
| 2v0 |
| ||
| v0 |
点评：粒子在电场中运动偏转时，常用能量的观点来解决问题，有时也要运用运动的合成与分解．粒子在磁场中做匀速圆周运动的圆心、半径及运动时间的确定也是本题的一个考查重点，要正确画出粒子运动的轨迹图，能熟练的运用几何知识解决物理问题．
练习册系列答案
阅读快车系列答案
相关题目
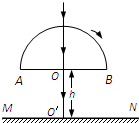（2013?常德模拟）如图所示，折射率n=
（2013?常德模拟）一交流发电机产生的感应电动势如图所示，其输出功率是40kW．现用5000V高压输电，输电线总电阻是4Ω，用户端利用n1：n2=250：11的变压器降压，则下列说法正确的是（ ）
（2013?常德模拟）静止在地面上的一小物体，在竖直向上的拉力作用下开始运动，在向上运动的过程中，物体的机械能与位移的关系图象如图所示，其中0～S1过程的图线是曲线，S1～S2过程的图线为平行于横轴的直线．关于物体上升过程（不计空气阻力）下列说法正确的是（ ）