题目内容
带电小球的质量为m,当匀强电场方向水平向右时,小球恰能静止在光滑圆槽形轨道的A点,图中角θ=30°,如图所示,当将电场方向转为竖直向下时(保持匀强电场的电场强度大小不变),求小球从A点起滑到最低点时对轨道的压力.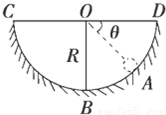
【答案】分析:当场强方向向右时,对小球在A点受力分析由平衡条件求得电场力大小.
小球从A到B的过程中,重力、电场力都做正功.由动能定理求得最低点速度大小,再根据牛顿第二定律求出小球到B点时受到的支持力,最后根据牛顿第三定律得出对轨道的压力.
解答: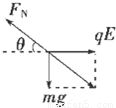 解:设小球带电量为q,电场强度大小为E,
解:设小球带电量为q,电场强度大小为E,
当场强方向向右时,小球在A点受力如图.
由平衡条件得:
qE=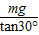 =
=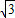 mg.
mg.
当场强方向竖直向下时,电场力的方向变为竖直向下,
小球从A到B的过程中,重力、电场力都做正功.
由动能定理得:
(mg+qE)R(1-sin30°)= mv2-0
mv2-0
∴v=
设小球到B点时受到的支持力为F′N.
则:F′N-(mg+qE)=
代入数据解得:
F′N=2( +1)mg
+1)mg
由牛顿第三定律知,小球对轨道的压力
F″N=2(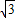 +1)mg,方向竖直向下.
+1)mg,方向竖直向下.
答:小球从A点起滑到最低点时对轨道的压力大小是2( +1)mg,方向竖直向下.
+1)mg,方向竖直向下.
点评:本题是力电综合问题,要明确小球的受力和运动情况,把动能定理和牛顿运动定律结合运用求解.
动能定理的优点在于适用任何运动包括曲线运动.
小球从A到B的过程中,重力、电场力都做正功.由动能定理求得最低点速度大小,再根据牛顿第二定律求出小球到B点时受到的支持力,最后根据牛顿第三定律得出对轨道的压力.
解答:
 解:设小球带电量为q,电场强度大小为E,
解:设小球带电量为q,电场强度大小为E,当场强方向向右时,小球在A点受力如图.
由平衡条件得:
qE=
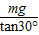 =
=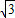 mg.
mg.当场强方向竖直向下时,电场力的方向变为竖直向下,
小球从A到B的过程中,重力、电场力都做正功.
由动能定理得:
(mg+qE)R(1-sin30°)=
 mv2-0
mv2-0∴v=

设小球到B点时受到的支持力为F′N.
则:F′N-(mg+qE)=

代入数据解得:
F′N=2(
 +1)mg
+1)mg由牛顿第三定律知,小球对轨道的压力
F″N=2(
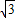 +1)mg,方向竖直向下.
+1)mg,方向竖直向下.答:小球从A点起滑到最低点时对轨道的压力大小是2(
 +1)mg,方向竖直向下.
+1)mg,方向竖直向下.点评:本题是力电综合问题,要明确小球的受力和运动情况,把动能定理和牛顿运动定律结合运用求解.
动能定理的优点在于适用任何运动包括曲线运动.

练习册系列答案
相关题目
 带电小球的质量为m,当匀强电场方向水平向右时,小球恰能静止在光滑圆槽形轨道的A点,图中角θ=30°,如图所示,当将电场方向转为竖直向下时(保持匀强电场的电场强度大小不变),求小球从A点起滑到最低点时对轨道的压力.
带电小球的质量为m,当匀强电场方向水平向右时,小球恰能静止在光滑圆槽形轨道的A点,图中角θ=30°,如图所示,当将电场方向转为竖直向下时(保持匀强电场的电场强度大小不变),求小球从A点起滑到最低点时对轨道的压力.
