题目内容
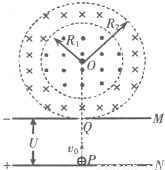
如图所示,M、N为加速电场的两极板,M板中心有一小孔Q,其正上方有一半径为R1=1m的圆形磁场区域,圆心为0,另有一内半径为R1,外半径为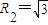 m的同心环形磁场区域,区域边界与M板相切于Q点,磁感应强度大小均为B=0.5T,方向相反,均垂直于纸面.一比荷
m的同心环形磁场区域,区域边界与M板相切于Q点,磁感应强度大小均为B=0.5T,方向相反,均垂直于纸面.一比荷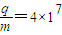 C/kg带正电粒子从N板的P点由静止释放,经加速后通过小孔Q,垂直进入环形磁场区域.已知点P、Q、O在同一竖直线上,不计粒子的重力,且不考虑粒子的相对论效应.
C/kg带正电粒子从N板的P点由静止释放,经加速后通过小孔Q,垂直进入环形磁场区域.已知点P、Q、O在同一竖直线上,不计粒子的重力,且不考虑粒子的相对论效应.(1)若加速电压
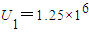 V,求粒子刚进入环形磁场时的速率v
V,求粒子刚进入环形磁场时的速率v(2)要使粒子能进入中间的圆形磁场区域,加速电压U2应满足什么条件?
(3)在某加速电压下粒子进入圆形磁场区域,恰能水平通过圆心O,之后返回到出发点P,求粒子从Q孔进人磁场到第一次回到Q点所用的时间.
【答案】分析:(1)根据动能定理列式求解即可;
(2)画出粒子恰好不进入中间磁场区的临界轨迹,先根据几何关系求出半径,然后根据洛伦兹力提供向心力列方程,再根据动能定理对直线加速过程列方程,最后联立方程组求解即可;
(3)画出运动轨迹并结合对称性,得到轨迹对应的圆心角,然后求解出时间.
解答:解:(1)粒子在匀强电场中,由动能定理得:
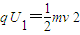 …①
…①
解得: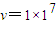 m/s…②
m/s…②
(2)粒子刚好不进入中间圆形磁场的轨迹如图所示,
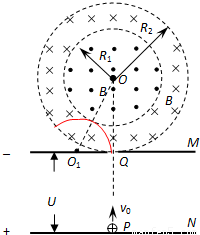
设此时粒子在磁场中运动的旋转半径为r1,在Rt△QOO1中有:
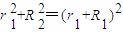 …③
…③
解得r1=1m…④
洛伦兹力提供向心力,有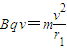 …⑤
…⑤
解得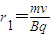
又由动能定理得: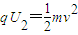 …⑥
…⑥
联立④⑤⑥得: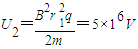 …⑦
…⑦
所以加速电压U2满足条件是:U2>5×106V…⑧
(3)粒子的运动轨迹如图所示
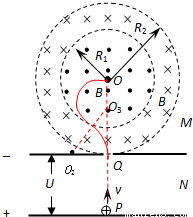
由于 O、O3、Q共线且竖直,又由于粒子在两磁场中的半径相同为r2,有
O2O3=2O2Q=2r2
由几何关系得∠QO2O3=60
故粒子从Q孔进入磁场到第一次回到Q点所用的时间为
t=2 ( T+
T+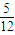 T )=
T )= T…⑨
T…⑨
又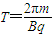 …⑩
…⑩
由⑨⑩得t≈3.66×10-7s
答:(1)粒子刚进入环形磁场时的速率为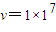 m/s;
m/s;
(2)要使粒子能进入中间的圆形磁场区域,加速电压U2应满足条件:U2>5×106V;
(3)粒子从Q孔进人磁场到第一次回到Q点所用的时间约为3.66×10-7s.
点评:本题关键分析清楚带电粒子的运动情况,明确粒子各个阶段的运动规律,然后结合动能定理、牛顿第二定律等规律列式求解.
(2)画出粒子恰好不进入中间磁场区的临界轨迹,先根据几何关系求出半径,然后根据洛伦兹力提供向心力列方程,再根据动能定理对直线加速过程列方程,最后联立方程组求解即可;
(3)画出运动轨迹并结合对称性,得到轨迹对应的圆心角,然后求解出时间.
解答:解:(1)粒子在匀强电场中,由动能定理得:
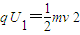 …①
…①解得:
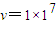 m/s…②
m/s…②(2)粒子刚好不进入中间圆形磁场的轨迹如图所示,

设此时粒子在磁场中运动的旋转半径为r1,在Rt△QOO1中有:
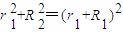 …③
…③解得r1=1m…④
洛伦兹力提供向心力,有
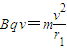 …⑤
…⑤解得
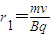
又由动能定理得:
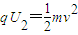 …⑥
…⑥联立④⑤⑥得:
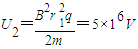 …⑦
…⑦所以加速电压U2满足条件是:U2>5×106V…⑧
(3)粒子的运动轨迹如图所示

由于 O、O3、Q共线且竖直,又由于粒子在两磁场中的半径相同为r2,有
O2O3=2O2Q=2r2
由几何关系得∠QO2O3=60
故粒子从Q孔进入磁场到第一次回到Q点所用的时间为
t=2 (
 T+
T+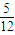 T )=
T )= T…⑨
T…⑨又
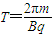 …⑩
…⑩由⑨⑩得t≈3.66×10-7s
答:(1)粒子刚进入环形磁场时的速率为
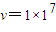 m/s;
m/s;(2)要使粒子能进入中间的圆形磁场区域,加速电压U2应满足条件:U2>5×106V;
(3)粒子从Q孔进人磁场到第一次回到Q点所用的时间约为3.66×10-7s.
点评:本题关键分析清楚带电粒子的运动情况,明确粒子各个阶段的运动规律,然后结合动能定理、牛顿第二定律等规律列式求解.

练习册系列答案
相关题目
 如图所示,M、N为水平位置的两块平行金属板,板间距离为d,两板间电势差为U.当带电量为q、质量为m的正离子流以速度V0沿水平方向从两板左端的中央O点处射入,因受电场力作用,离子作曲线运动,偏向M板(重力忽略不计).今在两板间加一匀强磁场,使从中央O处以速度V0射入的正离流在两板间作直线运动,求:所加匀强磁场的大小和方向?
如图所示,M、N为水平位置的两块平行金属板,板间距离为d,两板间电势差为U.当带电量为q、质量为m的正离子流以速度V0沿水平方向从两板左端的中央O点处射入,因受电场力作用,离子作曲线运动,偏向M板(重力忽略不计).今在两板间加一匀强磁场,使从中央O处以速度V0射入的正离流在两板间作直线运动,求:所加匀强磁场的大小和方向?
 如图所示,M、N为两块水平放置的平行金属板,板长为l,板间相距为d,两板间加有一电压,且M板电势高于N板。今有一质量为m、电荷量为-q的小球(视为质点)平行于两金属板、并沿两板中央直线以速度v水平飞入两板间,
如图所示,M、N为两块水平放置的平行金属板,板长为l,板间相距为d,两板间加有一电压,且M板电势高于N板。今有一质量为m、电荷量为-q的小球(视为质点)平行于两金属板、并沿两板中央直线以速度v水平飞入两板间,
