题目内容
6. 如图所示,两根足够长的“∧”形状的金属导轨构成两个斜面,斜面与水平面间夹角均为θ=37°,导轨间距L=1m,导轨电阻可忽略不计.两根相同的金属棒ab和a′b′的质量都为m=0.2kg,电阻R=1Ω,与导轨垂直放置且接触良好,金属棒和导轨之间的动摩擦因数μ=0.25,两个导轨斜面分别处于垂直于自身斜面向上的两匀强磁场中(图中未画出),磁感应强度B的大小相同.让a′b′在平行于斜面的外力F作用下保持静止,将金属棒ab由静止开始释放,当ab下滑速度达到稳定时,整个回路消耗的电功率为P=8W.g=10m/s2,sin 37°=0.6,cos 37°=0.8.求:
如图所示,两根足够长的“∧”形状的金属导轨构成两个斜面,斜面与水平面间夹角均为θ=37°,导轨间距L=1m,导轨电阻可忽略不计.两根相同的金属棒ab和a′b′的质量都为m=0.2kg,电阻R=1Ω,与导轨垂直放置且接触良好,金属棒和导轨之间的动摩擦因数μ=0.25,两个导轨斜面分别处于垂直于自身斜面向上的两匀强磁场中(图中未画出),磁感应强度B的大小相同.让a′b′在平行于斜面的外力F作用下保持静止,将金属棒ab由静止开始释放,当ab下滑速度达到稳定时,整个回路消耗的电功率为P=8W.g=10m/s2,sin 37°=0.6,cos 37°=0.8.求:(1)ab下滑的最大加速度;
(2)磁感应强度B的大小;
(3)ab下落了30m高度时,速度已经达到稳定,求此过程中回路电流的发热量Q.
分析 (1)对ab棒受力分析,由牛顿第二定律求最大加速度;
(2)根据平衡条件,结合电磁感应定律与闭合电路欧姆定律,及功率表达式,即可求解;
(3)ab下落了30m高度时,其下滑速度已经达到稳定,ab棒减小的重力势能转化为其动能、摩擦生热和焦耳热,根据能量守恒列式求回路电流的发热量Q.
解答 解:
(1)当ab棒刚下滑时,ab棒的加速度最大,设为a,则
mgsinθ-μmgcosθ=ma
解得:a=4m/s2
(2)ab棒达到最大速度vm时做匀速运动,设电动势为E,电流为I,则
mgsinθ=BIL+μmgcosθ
感应电动势:E=BLυm
感应电流:I=$\frac{E}{2R}$
功率表达式,P=EI
解得:vm=10m/s,
B=0.4T
(3)根据能量守恒得,有$mgh=\frac{1}{2}mυ_m^2+μmgcosθ•\frac{h}{sinθ}+Q$
解得:Q=30J
答:(1)ab下滑的最大加速度4m/s2;
(2)磁感应强度B的大小0.4T;
(3)ab下落了30m高度时,速度已经达到稳定,此过程中回路电流的发热量30J.
点评 本题是电磁感应与力学知识的综合,关键是计算安培力的大小和分析能量怎样转化,根据平衡条件和能量守恒进行研究.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.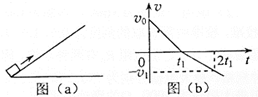 如图(a),一物块在t=0时刻滑上一固定斜面,其运动的v?t图线如图(b)所示.若重力加速度及图中的v0、v1、t1均为己知量,则不可求出( )
如图(a),一物块在t=0时刻滑上一固定斜面,其运动的v?t图线如图(b)所示.若重力加速度及图中的v0、v1、t1均为己知量,则不可求出( )
 如图(a),一物块在t=0时刻滑上一固定斜面,其运动的v?t图线如图(b)所示.若重力加速度及图中的v0、v1、t1均为己知量,则不可求出( )
如图(a),一物块在t=0时刻滑上一固定斜面,其运动的v?t图线如图(b)所示.若重力加速度及图中的v0、v1、t1均为己知量,则不可求出( )| A. | 斜面的倾角 | B. | 物块的质量 | ||
| C. | 物块与斜面间的动摩擦因数 | D. | 物块沿斜面向上滑行的最大高度 |
14. 远距离输电线路示意图如图所示,变压器均为理想变压器,发电机的输出电压及输电线的电阻均不变.则( )
远距离输电线路示意图如图所示,变压器均为理想变压器,发电机的输出电压及输电线的电阻均不变.则( )
 远距离输电线路示意图如图所示,变压器均为理想变压器,发电机的输出电压及输电线的电阻均不变.则( )
远距离输电线路示意图如图所示,变压器均为理想变压器,发电机的输出电压及输电线的电阻均不变.则( )| A. | 用户负载增加时,升压变压器的原线圈中电流不变 | |
| B. | 降压变压器的原线圈中电流较小,用较粗的导线绕制成 | |
| C. | 因为先升压后又要降压,所以不用变压器直接输电更节约电能 | |
| D. | 当用户用电器的总电阻增大时,输电线上损失的功率减小 |
16.关于核反应的类型,下列表述正确的有( )
| A. | ${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{8}^{17}$O+${\;}_{1}^{1}$H是β衰变 | |
| B. | ${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He是α衰变 | |
| C. | ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n是γ衰变 | |
| D. | ${\;}_{34}^{82}$Se→${\;}_{36}^{82}$Kr+2${\;}_{-1}^{0}$e是裂变 |
 一列简谐横波在同一均匀介质中传播,图甲为某时刻的波的图象,图乙为质点b从该时刻开始计时的振动图象.这列简谐波的传播速度为8m/s,质点d从该时刻起经过1.25s的路程为1m.
一列简谐横波在同一均匀介质中传播,图甲为某时刻的波的图象,图乙为质点b从该时刻开始计时的振动图象.这列简谐波的传播速度为8m/s,质点d从该时刻起经过1.25s的路程为1m. 如图所示水平传送带,轮的半径均为$\frac{1}{π}$,顺时针转动,两轮轴心相距L=8.0m.将一物体轻放在传送带左端,物体与传送带间的动摩擦因数为μ=0.4.
如图所示水平传送带,轮的半径均为$\frac{1}{π}$,顺时针转动,两轮轴心相距L=8.0m.将一物体轻放在传送带左端,物体与传送带间的动摩擦因数为μ=0.4. 如图所示,一根跨过一固定水平光滑细杆O的轻绳,两端各系一小球,球a置于地面,球b被拉到与细杆等高的位置,在绳刚被拉直时(无张力)释放b球,使b球由静止下摆,设两球质量相等,则a球刚要离开地面时,跨越细杆的两段绳之间的夹角为多少?
如图所示,一根跨过一固定水平光滑细杆O的轻绳,两端各系一小球,球a置于地面,球b被拉到与细杆等高的位置,在绳刚被拉直时(无张力)释放b球,使b球由静止下摆,设两球质量相等,则a球刚要离开地面时,跨越细杆的两段绳之间的夹角为多少?