题目内容
宇宙中，两颗靠得比较近的恒星，只受到彼此之间的万有引力作用互相绕转，称之为双星系统。设某双星系统绕其连线上的O点做匀速圆周运动，转动周期为T，轨道半径分别为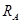
、
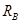且
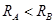，引力常量G已知，则下列说法正确的是（ ）
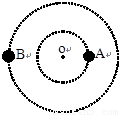
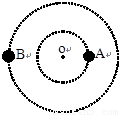
A．星体A的向心力大于星体B的向心力 宗
B．双星的角速度一定相同
C．星球A和星体B的质量之和为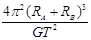
D．星球A的线速度一定大于星体B的线速度
【答案】
BC
【解析】
试题分析：彼此之间的万有引力作用互相绕转，所以两者的之间的向心力大小相等，A错误；两星绕同一点转动，故两星一直在同一直线上，故角速度相等，故B正确；设两颗恒星的质量分别为m1、m2，角速度分别为ω1，ω2．根据题意有
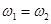①，根据万有引力定律和牛顿定律，有
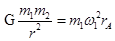②
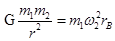③
联立以上各式解得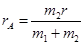
④
根据解速度与周期的关系知
⑤
联立③④⑤式解得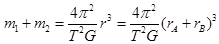
,C正确；
向心力相同，故两星的向心加速度不同，，半径不同，由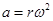
可得，线速度也不同，D错误
故选BC
考点：考查了双星问题
点评：双星问题要把握住双星的特点：彼此间的万有引力充当向心力，并且只能绕同一点做圆周运动．
练习册系列答案
相关题目
宇宙中，两颗靠得比较近的行星，只受到彼此之间的万有引力作用互相绕转，称之为双星系统，设某双星系统绕其连线上的O点做匀速圆周运动，如图所示．若AO＜OB，则（ ）
宇宙中，两颗靠得比较近的恒星，只受到彼此之间的万有引力作用互相绕转，称之为双星系统，设某双星系统绕其连线上的O点做匀速圆周运动，如图所示．若AO＜OB，则（ ）| A、双星的总质量一定，转动周期越小，双星之间的距离就越小 | B、星球A的向心力一定大于B的向心力 | C、星球A的质量一定小于B的质量 | D、星球A的线速度一定大于B的线速度 |
宇宙中，两颗靠得比较近的恒星，只受到彼此之间的万有引力作用互相绕转，称之为双星系统．设某双星系统绕其连线上的O点做匀速圆周运动，转动周期为T，轨道半径分别为RA、RB且RA＜RB，引力常量G已知，则下列说法正确的是（ ）| A、星体A的向心力大于星体B的向心力 宗 | ||
| B、双星的角速度一定相同 | ||
C、星球A和星体B的质量之和为
| ||
| D、星球A的线速度一定大于星体B的线速度 |
宇宙中，两颗靠得比较近的恒星，只受到彼此之间的万有引力作用互相绕转，称之为双星系统．在浩瀚的银河系中，多数恒星都是双星系统．设某双星系统A、B绕其连线上的O点做匀速圆周运动，如图所示．若AO>OB，则( )
| A．星球A的质量一定大于B的质量 |
| B．星球A的线速度一定大于B的线速度 |
| C．双星间距离一定，双星的质量越大，其转动周期越大 |
| D．双星的质量一定，双星之间的距离越大，其转动周期越大 |
宇宙中，两颗靠得比较近的恒星，只受到彼此之间的万有引力作用互相绕转，称之为双星系统。设某双星系统绕其连线上的O点做匀速圆周运动，转动周期为T，轨道半径分别为
、
且
，引力常量G已知，则下列说法正确的是（ ）
| A．星体A的向心力大于星体B的向心力 宗 |
| B．双星的角速度一定相同 |
C．星球A和星体B的质量之和为 |
| D．星球A的线速度一定大于星体B的线速度 |