题目内容
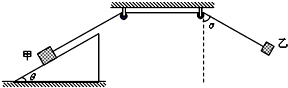 在如图所示的装置中,两个光滑的定滑轮的半径很小,表面粗糙的斜面固定在地面上,斜面的倾角为θ=30°.用一根跨过定滑轮的细绳连接甲、乙两物体,把甲物体放在斜面上且连线与斜面平行,把乙物体悬在空中,并使悬线拉直且偏离竖直方向α=60°.现同时释放甲、乙两物体,乙物体将在竖直平面内振动,当乙物体运动经过最高点和最低点时,甲物体在斜面上均恰好未滑动.已知乙物体的质量为m=1㎏,若取重力加速度g=10m/s2.求:甲物体的质量及斜面对甲物体的最大静摩擦力.
在如图所示的装置中,两个光滑的定滑轮的半径很小,表面粗糙的斜面固定在地面上,斜面的倾角为θ=30°.用一根跨过定滑轮的细绳连接甲、乙两物体,把甲物体放在斜面上且连线与斜面平行,把乙物体悬在空中,并使悬线拉直且偏离竖直方向α=60°.现同时释放甲、乙两物体,乙物体将在竖直平面内振动,当乙物体运动经过最高点和最低点时,甲物体在斜面上均恰好未滑动.已知乙物体的质量为m=1㎏,若取重力加速度g=10m/s2.求:甲物体的质量及斜面对甲物体的最大静摩擦力.分析:当乙物体运动到最高点时,拉力最小,此时甲物体有沿斜面向上的最大静摩擦力;当乙物体运动到最低点时,拉力最大,此时甲物体有沿斜面向下的最大静摩擦力,根据共点力平衡列出表达式,求出甲物体的质量和最大静摩擦力.
解答:解:设甲物体的质量为M,所受的最大静摩擦力为f,则当乙物体运动到最高点时,绳子上的弹力最小,设为T1,
对乙物体 T1=mgcosα
此时甲物体恰好不下滑,有:Mgsinθ=f+T1
得:Mgsinθ=f+mgcosα
当乙物体运动到最低点时,设绳子上的弹力最大,设为T2
对乙物体由动能定理:mgl(1-cosα)=
mv2
又由牛顿第二定律:T2-mg=m
此时甲物体恰好不上滑,则有:Mgsinθ+f=T2
得:Mgsinθ+f=mg(3-2cosα)
可解得:M=2.5kg
f=7.5N.
故物体的质量为2.5kg,斜面对甲物体的最大静摩擦力为7.5N.
对乙物体 T1=mgcosα
此时甲物体恰好不下滑,有:Mgsinθ=f+T1
得:Mgsinθ=f+mgcosα
当乙物体运动到最低点时,设绳子上的弹力最大,设为T2
对乙物体由动能定理:mgl(1-cosα)=
| 1 |
| 2 |
又由牛顿第二定律:T2-mg=m
| v2 |
| l |
此时甲物体恰好不上滑,则有:Mgsinθ+f=T2
得:Mgsinθ+f=mg(3-2cosα)
可解得:M=2.5kg
f=7.5N.
故物体的质量为2.5kg,斜面对甲物体的最大静摩擦力为7.5N.
点评:本题是动能定理和动力学结合的问题,关键找出两个临界状态.在两个临界状态下甲物体处于平衡状态.

练习册系列答案
相关题目
 在如图所示的装置中,A、B、C、D为四个平行正对的金属板,其中B板和C板上开有小孔,分别与两个电源相连,B和A两板间的电压为U,C和D两板间电压为2U,从靠近A板的F处释放出一个无初速度的电子,电荷量为e.关于电子的运动,下列描述中哪些是正确的( )
在如图所示的装置中,A、B、C、D为四个平行正对的金属板,其中B板和C板上开有小孔,分别与两个电源相连,B和A两板间的电压为U,C和D两板间电压为2U,从靠近A板的F处释放出一个无初速度的电子,电荷量为e.关于电子的运动,下列描述中哪些是正确的( ) (2011?广元模拟)在如图所示的装置中,电源电动势为E,内阻不计,定值电阻为R1,滑动变阻器总值为R2,置于真空中的平行板电容器水平放置,极板间距为d.处在电容器中的油滴A恰好静止不动,此时滑动变阻器的滑片P位于中点位置.
(2011?广元模拟)在如图所示的装置中,电源电动势为E,内阻不计,定值电阻为R1,滑动变阻器总值为R2,置于真空中的平行板电容器水平放置,极板间距为d.处在电容器中的油滴A恰好静止不动,此时滑动变阻器的滑片P位于中点位置. 在如图所示的装置中,木块B与水平桌面的接触是光滑的,子弹A沿水平方向射入木块后留在木块内.从子弹射向木块到木块将弹簧压缩到最短的全过程中,下列说法正确
在如图所示的装置中,木块B与水平桌面的接触是光滑的,子弹A沿水平方向射入木块后留在木块内.从子弹射向木块到木块将弹簧压缩到最短的全过程中,下列说法正确 (2007?苏州二模)处在激发态的氢原子向能量较低的状态跃迁时会发出一系列不同频率的光,称为氢光谱.氢光谱线的波长可以用下面的巴耳末-里德伯公式
(2007?苏州二模)处在激发态的氢原子向能量较低的状态跃迁时会发出一系列不同频率的光,称为氢光谱.氢光谱线的波长可以用下面的巴耳末-里德伯公式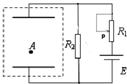 在如图所示的装置中,电源电动势为E,内阻不计,R2为定值电阻,滑动变阻器的滑片P位于中点位置时油滴A恰好静止不动,如将滑片P向下滑,油滴将( )
在如图所示的装置中,电源电动势为E,内阻不计,R2为定值电阻,滑动变阻器的滑片P位于中点位置时油滴A恰好静止不动,如将滑片P向下滑,油滴将( )