题目内容
 (2007?苏州二模)处在激发态的氢原子向能量较低的状态跃迁时会发出一系列不同频率的光,称为氢光谱.氢光谱线的波长可以用下面的巴耳末-里德伯公式
(2007?苏州二模)处在激发态的氢原子向能量较低的状态跃迁时会发出一系列不同频率的光,称为氢光谱.氢光谱线的波长可以用下面的巴耳末-里德伯公式| 1 |
| λ |
| 1 |
| k2 |
| 1 |
| n2 |
在如图所示的装置中,K为一金属板,A为金属电极,都密封在真空的玻璃管中,S为由石英片封盖的窗口,单色光可通过石英片射到金属板K上,E为输出电压可调的直流电源,开始时其负极与电极A相连.实验发现,当用某种频率的单色光照射K时,K会发出电子(光电效应),这时,即使A、K之间的电压等于零,回路中也有电流.当A的电势低于K时,而且当A比K的电势低到某一值Uc时,电流消失,Uc称为遏止电压.
用氢原子发出的光照射某种金属进行光电效应实验时发现:当用赖曼系波长最长的光照射时,遏止电压的大小为U1,当用巴耳末系波长最短的光照射时,遏止电压的大小为U2,已知电子电荷量的大小为e,真空中的光速为c,普朗克常数为h,试求
(1)赖曼系波长最长的光所对应的光子的能量.
(2)巴耳末系波长最短的光所对应的光子的能量.
(3)该种金属的逸出功W(用电子电荷量e与测量值U1、U2表示).
分析:(1)根据巴耳末-里德伯公式可知赖曼系波长最长的光是氢原子由n=2→k=1跃迁时发出的,由该公式求出波长λ,光子能量E=hγ=h
.
(2)巴耳末系波长最短的光是氢原子由n=∞→k=2跃迁时发出的,由该公式求出波长λ,并求出对应光子的能量.
(3)根据两次光电效应中遏止电压,根据爱因斯坦光电效应方程列式,组成方程组求解金属的逸出功W.
| c |
| λ |
(2)巴耳末系波长最短的光是氢原子由n=∞→k=2跃迁时发出的,由该公式求出波长λ,并求出对应光子的能量.
(3)根据两次光电效应中遏止电压,根据爱因斯坦光电效应方程列式,组成方程组求解金属的逸出功W.
解答:解:(1)根据巴耳末-里德伯公式可知赖曼系波长最长的光是氢原子由n=2→k=1跃迁时发出的,由该公式得:波长λ12=
R,
对应的光子能量为 E12=hc
联立解得,E12=
,式中h是普朗克常量.
(2)巴耳末系波长最短的光是氢原子由n=∞→k=2跃迁时发出的,则
波长λ2∞=
R,
对应的光子能量为 E2∞=
.
(3)由爱因斯坦光电效应方程得:
=eU1+W
=eU2+W
联立上两式得 W=
(U1-3U2)
答:
(1)赖曼系波长最长的光所对应的光子的能量是
.
(2)巴耳末系波长最短的光所对应的光子的能量是
.
(3)该种金属的逸出功W是
(U1-3U2).
| 3 |
| 4 |
对应的光子能量为 E12=hc
| 1 |
| λ12 |
联立解得,E12=
| 3Rhc |
| 4 |
(2)巴耳末系波长最短的光是氢原子由n=∞→k=2跃迁时发出的,则
波长λ2∞=
| 1 |
| 4 |
对应的光子能量为 E2∞=
| Rhc |
| 4 |
(3)由爱因斯坦光电效应方程得:
| 3Rhc |
| 4 |
| Rhc |
| 4 |
联立上两式得 W=
| e |
| 2 |
答:
(1)赖曼系波长最长的光所对应的光子的能量是
| 3Rhc |
| 4 |
(2)巴耳末系波长最短的光所对应的光子的能量是
| Rhc |
| 4 |
(3)该种金属的逸出功W是
| e |
| 2 |
点评:本题玻尔理论与光电效应的综合应用,关键要掌握光电效应的规律和玻尔理论,读懂题意,从大量材料中获取有效信息.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 (2007?苏州二模)如图所示,“U”形金属框架固定在水平面上,金属杆ab与框架间无摩擦.整个装置处于竖直方向的磁场中.若因磁场的变化,使杆ab向右运动,则磁感应强度( )
(2007?苏州二模)如图所示,“U”形金属框架固定在水平面上,金属杆ab与框架间无摩擦.整个装置处于竖直方向的磁场中.若因磁场的变化,使杆ab向右运动,则磁感应强度( ) (2007?苏州二模)两束单色光a和b同时由空气射到某介质的界面MN上,由于折射而合成一复色光c,如图所示.下列说法中正确的是( )
(2007?苏州二模)两束单色光a和b同时由空气射到某介质的界面MN上,由于折射而合成一复色光c,如图所示.下列说法中正确的是( )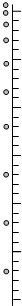 (2007?苏州二模)在学到自由落体这一部分内容后,有同学计算,若有雨滴从距地面2.5km高空自由落下,到达地面时速度将达到700m/s.这雨滴无异于一发高速运动的子弹.事实上谁也未见过如此高速的雨滴,这引发了一些同学的思考:雨滴在下落时肯定受到了空气阻力的作用.哪它究竟是如何运动的呢?有一组同学设计了一个实验,用胶木球在水中的自由下落来模拟雨滴在空气中的下落过程.实验中,胶木球从某一高度竖直落下,用闪光照相方法拍摄了小球在不同时刻的位置,如图所示.
(2007?苏州二模)在学到自由落体这一部分内容后,有同学计算,若有雨滴从距地面2.5km高空自由落下,到达地面时速度将达到700m/s.这雨滴无异于一发高速运动的子弹.事实上谁也未见过如此高速的雨滴,这引发了一些同学的思考:雨滴在下落时肯定受到了空气阻力的作用.哪它究竟是如何运动的呢?有一组同学设计了一个实验,用胶木球在水中的自由下落来模拟雨滴在空气中的下落过程.实验中,胶木球从某一高度竖直落下,用闪光照相方法拍摄了小球在不同时刻的位置,如图所示.