题目内容
如图所示,光滑斜面倾角为 ,c为斜面上固定挡板,物块a和b通过轻质弹簧连接,a、b处于静止状态,弹簧压缩量为x.现对a施加沿斜面向下的外力使弹簧再压缩2x,之后突然撤去外力,经时间t,物块a沿斜面向上运动的速度为
,c为斜面上固定挡板,物块a和b通过轻质弹簧连接,a、b处于静止状态,弹簧压缩量为x.现对a施加沿斜面向下的外力使弹簧再压缩2x,之后突然撤去外力,经时间t,物块a沿斜面向上运动的速度为 ,此时物块刚要离开挡板。已知两物块的质量均为m,重力加速度为g,下列说法正确的是( )
,此时物块刚要离开挡板。已知两物块的质量均为m,重力加速度为g,下列说法正确的是( )

A.弹簧的劲度系数为
B.物块b刚要离开挡板时,a的加速度为
C.物块a沿斜面向上运动速度最大时,物块b对挡板c的压力为0
D.撤去外力后,经过时间t,弹簧弹性势能变化量大小为
【答案】
D
【解析】
试题分析:a、b处于静止状态,弹簧压缩量为x,对a而言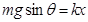 ,所以A错。物块b刚要离开挡板时说明挡板支持力为0,而此刻b物体还没有运动,可看作平衡,即
,所以A错。物块b刚要离开挡板时说明挡板支持力为0,而此刻b物体还没有运动,可看作平衡,即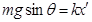 ,此刻对a而言,弹簧拉力向下所以此时a的合外力为
,此刻对a而言,弹簧拉力向下所以此时a的合外力为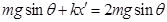 ,所以加速度为
,所以加速度为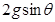 ,方向向下,B错。由于物块b对挡板c的压力为0时a加速度已经向下,所以a已经减速一段时间,所以此刻速度肯定不是最大,C错。根据动能定理
,方向向下,B错。由于物块b对挡板c的压力为0时a加速度已经向下,所以a已经减速一段时间,所以此刻速度肯定不是最大,C错。根据动能定理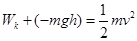 ,其中
,其中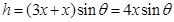 ,所以弹力做功为
,所以弹力做功为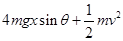 即弹性势能变化量为
即弹性势能变化量为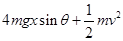 ,D对
,D对
考点:受力分析、动能定理
点评:此类题型考察了受力分析并利用题目中的条件分析出关键条件即挡板对b支持力为零,利用动能定理求解。

练习册系列答案
相关题目
 如图所示,一个质量分布均匀的球放在互成120°的两块光滑平面上保持静止状态OA是水平面,OB是倾斜面,关于球的受力,下列说法正确的是( )
如图所示,一个质量分布均匀的球放在互成120°的两块光滑平面上保持静止状态OA是水平面,OB是倾斜面,关于球的受力,下列说法正确的是( )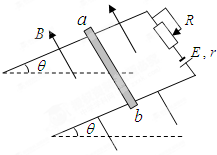 如图所示,在倾θ=30°的绝缘斜面上,固定一L=0.25m的平行金属导轨,在导轨上端接入电源和滑动变阻器,电源电动E=12V,内r=1Ω,一质m=20g的金属ab与两导轨垂直并接触良好,整个装置处于磁感应强B=0.8T,方向垂直于斜面向上的匀强磁场中.金属导轨光滑,导轨与金属棒的电阻不计,g=10m/s2,要保持金属棒在导轨上静止,求:
如图所示,在倾θ=30°的绝缘斜面上,固定一L=0.25m的平行金属导轨,在导轨上端接入电源和滑动变阻器,电源电动E=12V,内r=1Ω,一质m=20g的金属ab与两导轨垂直并接触良好,整个装置处于磁感应强B=0.8T,方向垂直于斜面向上的匀强磁场中.金属导轨光滑,导轨与金属棒的电阻不计,g=10m/s2,要保持金属棒在导轨上静止,求: 如图所示,粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾a=37°,A、B、C是三个小滑块(可看做质点),A、B的质量均为m=1kg,B的左端附有胶泥(质量不计),C的质量均为M=2kg,D为两端分别连接B和C的轻质弹簧.
如图所示,粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾a=37°,A、B、C是三个小滑块(可看做质点),A、B的质量均为m=1kg,B的左端附有胶泥(质量不计),C的质量均为M=2kg,D为两端分别连接B和C的轻质弹簧.
