题目内容
如图所示,足够长的水平传送带以速度v沿逆时针方向转动,传送带的左端与光滑圆弧轨道底部平滑连接,圆弧轨道上的A点与圆心等高,一小物块从A点静止滑下,再滑上传送带,经过一段时间又返回圆弧轨道,返回圆弧轨道时小物块恰好能到达A点,则下列说法正确的是（?? ）
A.圆弧轨道的半径一定是v2/2g
B.若减小传送带速度,则小物块不可能到达A点
C.若增加传送带速度,则小物块有可能经过圆弧轨道的最高点
D.不论传送带速度增加到多大,小物块都不可能经过圆弧轨道的最高点??
【答案】
D
【解析】
试题分析：在圆轨道上下滑过程，设物块滑上传送带的初速度 v0，根据机械能守恒可得，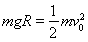
，
物体到达传送带上之后，在滑动摩擦力的作用做减速运动，速度减小为零之后，又在滑动摩擦力的作用下反向加速，根据牛顿第二定律可知，物体在减速和加速的过程物体的加速度的大小是相同的，当传送带的速度v≥v0时，物体返回圆轨道时速度大小等于v0，物体能返回A点，与半径R无关，所以A错误；减小传送带速度v，使v≥v0，小物块可以到达A点，故B错误；若增大传送带的速度，由于物体返回到圆轨道的速度不变，只能滑到A点，不能滑到圆弧轨道的最高点，故C错误；D正确。
考点：本题考查牛顿运动定律、匀变速运动的规律
练习册系列答案
相关题目
如图所示．质量为M的平板小车停在光滑的水平面上．小车的右端有一固定挡板，挡板上固定一长度足够长的水平弹簧．弹簧的自然端伸长的B点．小车上B点左边是粗糙的，B点至小车左端A的距离为l，B点右边是光滑的．现有一质量为m的小滑块（可视为质点）以初速度v0水平滑上小车，在滑块滑上小车直到将弹簧压缩至最短的过程中将小车锁定，当弹簧压缩至最短时刻解除锁定．最终滑块与小车相对静止，滑块恰好停在AB的中点．问滑块与小车AB段间的动摩擦力因素为多少？
如图所示，一圆柱形容器上部圆筒较细，下部的圆筒较粗且足够长．容器的底是一可沿下圆筒无摩擦移动的活塞S，用细绳通过测力计F将活塞提着，容器中盛水．开始时，水面与上圆筒的开口处在同一水平面上（如图），在提着活塞的同时使活塞缓慢地下移．在这一过程中，测力计的读数（ ）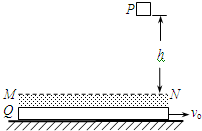
如图所示，P为质量为m=1kg的物块，Q为位于水平地面上的质量为M=4kg的特殊平板，平板与地面间的动摩因数μ=0.02．在板上表面的上方，存在一定厚度的“相互作用区域”，区域的上边界为MN．P刚从距高h=5m处由静止开始自由落下时，板Q向右运动的速度为vo=4m/s．当物块P进入相互作用区域时，P、Q之间有相互作用的恒力F=kmg，其中Q对P的作用竖直向上，k=21，F对P的作用使P刚好不与Q的上表面接触．在水平方向上，P、Q之间没有相互作用力，板Q足够长，空气阻力不计．（ 取g=10m/s2，以下计算结果均保留两位有效数字）求：
A． 在A、C两点以相同的速度同时水平向右抛出两小球，两球一定会相遇