题目内容
14．一个质量为20kg的小孩从距地面高为3m，长为6m的滑梯顶端由静止开始滑下，滑到底端时的速度为2m/s，g=10m/s2，关于力对小孩做功说法正确的是（ ）| A． | 重力做功1200J | B． | 合力做功40J | ||
| C． | 阻力做功为‐1160J | D． | 支持力做功40J |
分析 根据动能定理求解合外力做功和阻力做功．根据小孩高度的变化求解重力做功．根据支持力与位移方向间的关系分析支持力做功情况．
解答 解：A、重力做功为WG=mgh=20×10×3=600J．故A错误；
B、由动能定理合外力做的功等于动能的变化量，W合=$\frac{1}{2}$mv2=$\frac{1}{2}$×20×22=40J，故B正确；
C、根据动能定理：WG-Wf=40J
则Wf=560J，故C错误；
D、支持力与小孩的运动方向始终垂直，故支持力不做功，D错误；
故选：B
点评 本题考查对功的计算两种方法的掌握情况：一种恒力做功根据功的公式计算功；二是根据动能定理计算功．
练习册系列答案
名校课堂系列答案
相关题目
某校开展研究性学习，某研究小组根据光学知识，设计了一个测液体折射率的仪器．如图，在一个圆盘上，过其圆心O作两条相互垂直的直径BC、EF．在半径OA上，垂直盘面插上两枚大头针P1、P2并保持位置不变．每次测量时让圆盘的下半部分竖直进入液体中，而且总使得液面与直径BC相平，EF作为界面的法线，而后在图中右上方区域观察P1、P2．同学们通过计算，预先在圆周EC部分刻好了折射率的值，这样只要根据P3所插的位置，就可以直接读出液体折射率的值．
一位链球运动员在水平面内旋转质量为4kg的链球，链球每1s转一圈，转动半径为1.5m，求：
2．
如图所示，实线为等量异号点电荷周围的电场线，虚线为以一点电荷为中心的圆，M点是两点电荷连线的中点．若将一试探正点电荷从虚线上N点沿虚线移动到M点，则（ ）
如图所示，实线为等量异号点电荷周围的电场线，虚线为以一点电荷为中心的圆，M点是两点电荷连线的中点．若将一试探正点电荷从虚线上N点沿虚线移动到M点，则（ ）| A． | 电荷所受电场力大小不变 | B． | 电荷所受电场力逐渐变大 | ||
| C． | 电荷电势能逐渐减小 | D． | 电荷电势能逐渐增大 |
图为ARJ21-700飞机在上海成功实现首飞的雄姿，它是中国首架自主研制、拥有完全自主知识产权的新型涡扇支线飞机．飞机的质量为m，以水平速度v0飞离跑道后逐渐上升，假定在此过程中水平速度保持不变，竖直方向可认为是匀加速运动．飞机从飞离地面后开始算起，测得它在水平方向发生的位移为s时，在竖直方向上升的高度为h．求：
19．
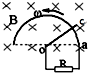如图所示，在磁感强度为B的匀强磁场中，有半径为r的光滑半圆形导体框架，OC为一能绕O在框架上滑动的导体棒，OC之间连一个电阻R，导体框架与导体棒的电阻均不计，若要使OC能以角速度ω匀速转动，则外力做功的功率是（ ）
如图所示，在磁感强度为B的匀强磁场中，有半径为r的光滑半圆形导体框架，OC为一能绕O在框架上滑动的导体棒，OC之间连一个电阻R，导体框架与导体棒的电阻均不计，若要使OC能以角速度ω匀速转动，则外力做功的功率是（ ）| A． | $\frac{{B}^{2}{r}^{2}{ω}^{4}}{4R}$ | B． | $\frac{{B}^{2}{r}^{4}{ω}^{2}}{4R}$ | C． | $\frac{{B}^{2}{r}^{4}{ω}^{2}}{2R}$ | D． | $\frac{{B}^{2}{r}^{4}{ω}^{2}}{9R}$ |
某同学在“探究平抛运动的规律”的实验中，用一张印有小方格的纸记录轨迹，在方格纸上建立如图所示的坐标系，小方格的边长L=6.4cm，若小球在平抛运动实验中记录了几个位置如图中的a、b、c、d、e 所示．（g=10m/s2）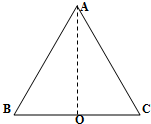
如图所示为一等边三角形的某种透明介质ABC，边长为L，折射率为$\frac{5}{3}$，底部中点O处有一点光源，试问能够从AB边射出光线的长度是多少？
如图所示，有一个边界为正三角形的匀强磁场区域，边长为a，磁感应强度方向垂直纸面向里，一个矩形导体框的长为a、宽为．若导体框平行于纸面沿着磁场区域的轴线匀速穿越磁场区域，取导体框中感应电流的逆时针方向为正方向，以导体框刚进入磁场时为t=0时刻．则在穿过磁场的过程中，导体框中的感应电流随时间变化的图象是图中的（ ）
