题目内容
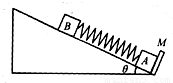
如图所示，一倾角为30°的光滑斜面底端有一与斜面垂直的固定挡板M，物块A、B之间用一与斜面平行轻质弹簧连结，现用力缓慢沿斜面向下推动物块B，当弹簧具有5J弹性势能时撤去推力释放物块B；已知A、B质量分别为mA=5kg、mB=2kg，弹簧的弹性势能表达式为E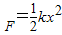
，其中弹簧的劲度系数k=1000N/m，x为弹簧形变量，g=10m/s2，求：（1）当弹簧恢复原长时，物块B的速度大小；
（2）物块A刚离开挡板时，物块B的动能．
【答案】分析：（1）弹簧减小的弹性势能等于物块B增加的机械能，根据守恒定律列式求解；
（2）物块A刚离开挡板时，受重力、斜面支持力和弹簧的拉力，根据平衡条件求解出拉力；根据胡克定律求解弹簧的伸长量，最后根据减小的弹性势能等于物块B增加的机械能列式求解．
解答：解：（1）当Ep=5J时，弹簧压缩x1，由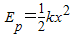
得x1=0.1m
当弹簧恢复原长时，由机械能守恒可得
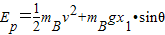
v=2m/s
（2）当物块A刚离开挡板时，弹簧伸长x2，根据共点力平衡条件，有：
kx2=mAg?sinθ
x2=0.025m
由系统机械能守恒得
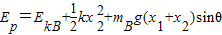
解得EkB=3.44J
答：（1）当弹簧恢复原长时，物块B的速度大小为2m/s；
（2）物块A刚离开挡板时，物块B的动能为3.44J．
点评：本题关键明确系统机械能守恒，要考虑弹性势能、重力势能、动能三种能量的转化，不难．
（2）物块A刚离开挡板时，受重力、斜面支持力和弹簧的拉力，根据平衡条件求解出拉力；根据胡克定律求解弹簧的伸长量，最后根据减小的弹性势能等于物块B增加的机械能列式求解．
解答：解：（1）当Ep=5J时，弹簧压缩x1，由
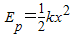得x1=0.1m 当弹簧恢复原长时，由机械能守恒可得
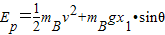
v=2m/s
（2）当物块A刚离开挡板时，弹簧伸长x2，根据共点力平衡条件，有：
kx2=mAg?sinθ
x2=0.025m
由系统机械能守恒得
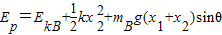
解得EkB=3.44J
答：（1）当弹簧恢复原长时，物块B的速度大小为2m/s；
（2）物块A刚离开挡板时，物块B的动能为3.44J．
点评：本题关键明确系统机械能守恒，要考虑弹性势能、重力势能、动能三种能量的转化，不难．
练习册系列答案
相关题目
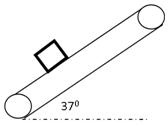
（2010?闵行区三模）如图所示，一倾角为37°的斜面固定在水平地面上，质量m=1kg的物体在平行于斜面向上的恒力F作用下，从A点由静止开始运动，到达B点时立即撤去拉力F．此后，物体到达C点时速度为零．每隔0.2s通过速度传感器测得物体的瞬时速度，下表给出了部分测量数据．（取 sin37°=0.6．cos37°=0.8）试求：
（2011?普陀区二模）如图所示，一倾角为37°的斜面固定在水平地面上，质量为1千克的物体在平行于斜面向上的恒力F作用下，从斜面的底端A点由静止开始运动，到达B点时立即撤去拉力F．此后，物体到达最高点C．每隔0.2s通过位移传感器测得物体的瞬时速度的大小，下表给出了部分测量数据．（取sin37°=0.6，cos37°=0.8）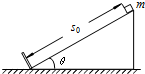
如图所示，一倾角为θ=37°的光滑斜面固定在地面上，斜面长度s0=3.0m，斜面底端有一垂直于斜面的固定挡板．在斜面顶端由静止释放一质量m=0.10kg的小物块．当小物块与挡板第一次碰撞后，能沿斜面上滑的最大距离s=0.75m．已知小物块第一次与挡板碰撞过程中从接触到离开所用时间为0.10s，重力加速度g取10m/s2，sin37°=0.6，cos37°=0.8．求：
如图所示，一倾角为30°的光滑斜面与水平地面平滑连接，水平地面的动摩擦因数为0.25，前方距离斜面底端B点10m处有一个障碍物Q．现有一小孩从斜面上h=3m高处的A点由静止开始滑下，不计小孩到斜面底端时受到的冲击（即到达B点前后瞬间速度大小不变），取g=10m/s2，试回答下列问题：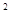
,sin37o=0.6,cos37o=0.8.）求：