Question

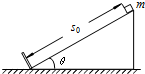如图所示，一倾角为θ=37°的光滑斜面固定在地面上，斜面长度s₀=3.0m，斜面底端有一垂直于斜面的固定挡板．在斜面顶端由静止释放一质量m=0.10kg的小物块．当小物块与挡板第一次碰撞后，能沿斜面上滑的最大距离s=0.75m．已知小物块第一次与挡板碰撞过程中从接触到离开所用时间为0.10s，重力加速度g取10m/s²，sin37°=0.6，cos37°=0.8．求：
（1）小物块第一次与挡板碰撞前的速度大小；
（2）小物块第一次与挡板撞击过程中损失的机械能；
（3）小物块第一次与挡板撞击过程中受到挡板的平均作用力．

Answer 1

分析：小物块下滑过程中，只有重力做功，根据机械能守恒可求碰前是速度
根据能量守恒可求碰撞过程中系统损失的机械能；
碰后上滑过程，机械能守恒，可求碰后的速度，根据动量定理可求碰撞过程中挡板的平均作用力

解答：解：（1）小物块下滑过程中，只有重力做功，根据机械能守恒：mgs₀sin37°=

1

2

mv2
可得：碰撞前的速度v=6m/s
（2）根据能量守恒可求碰撞过程中系统损失的机械能：△E=mgsin37°（s₀-s）
代入数据，得△E=1.35J
（3）碰后上滑过程，机械能守恒，
故mgssin37°=

1

2

mv′2
故碰后上滑的速度v′=3m/s
根据动量定理可得：Ft=mv′-（-mv），取沿斜面向上为正方向
可得F=9N，
答：（1）小物块第一次与挡板碰撞前的速度为6.0m/s
（2）小物块第一次与挡板撞击过程中损失的机械能1.35J
（3）小物块第一次与挡板撞击过程中受到挡板的平均作用力为9N，方向沿斜面向上．

点评：本题关键分析物块的运动状态，根据机械能守恒和动量定理列式求解．