题目内容
如图所示,玻璃球的半径为R,折射率n=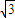 ,今有一束平行光沿直径AB方向照射在玻璃球上,试求离AB多远的入射光线最终射出后沿原方向返回.
,今有一束平行光沿直径AB方向照射在玻璃球上,试求离AB多远的入射光线最终射出后沿原方向返回.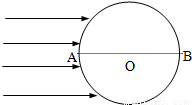
【答案】分析:由题,光线照射在玻璃球上,最终要能沿原方向相反方向射出,入射光路与出射光路必须对称,作出光路图,由几何知识得到入射角θ1与折射角θ2的关系,由折射定律n=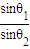 求出θ1与θ2.再由几何关系求出射出的光线离AB的距离.
求出θ1与θ2.再由几何关系求出射出的光线离AB的距离.
解答: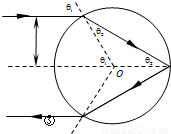 解:由题意分析:光线照射在玻璃球上,最终能沿原方向相反方向射出,说明入射光路与出射光路平行对称,作出光路图,由光路图知θ1=2θ2 ①
解:由题意分析:光线照射在玻璃球上,最终能沿原方向相反方向射出,说明入射光路与出射光路平行对称,作出光路图,由光路图知θ1=2θ2 ①
又根据折射定律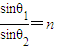 ②
②
解①②式得 cosθ2=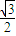 即 θ2=30°,θ1=60° ③
即 θ2=30°,θ1=60° ③
∵d=Rsinθ1 ④
∴d=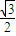 R ⑤
R ⑤
答:离AB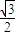 R远的入射光线最终射出后沿原方向返回.
R远的入射光线最终射出后沿原方向返回.
点评:本题的解题关键是抓住光路的对称性,画出光路图,再几何知识确定出入射角与折射角的关系,进行求解.
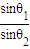 求出θ1与θ2.再由几何关系求出射出的光线离AB的距离.
求出θ1与θ2.再由几何关系求出射出的光线离AB的距离.解答:
 解:由题意分析:光线照射在玻璃球上,最终能沿原方向相反方向射出,说明入射光路与出射光路平行对称,作出光路图,由光路图知θ1=2θ2 ①
解:由题意分析:光线照射在玻璃球上,最终能沿原方向相反方向射出,说明入射光路与出射光路平行对称,作出光路图,由光路图知θ1=2θ2 ①又根据折射定律
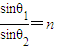 ②
②解①②式得 cosθ2=
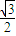 即 θ2=30°,θ1=60° ③
即 θ2=30°,θ1=60° ③∵d=Rsinθ1 ④
∴d=
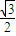 R ⑤
R ⑤答:离AB
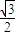 R远的入射光线最终射出后沿原方向返回.
R远的入射光线最终射出后沿原方向返回.点评:本题的解题关键是抓住光路的对称性,画出光路图,再几何知识确定出入射角与折射角的关系,进行求解.

练习册系列答案
相关题目
 (2013?太原一模)两束平行的细激光束,垂直于半球形玻璃体的圆平面射到半圆球体上,如图所示.已知其中一条光线沿直线穿过玻璃,它的入射点是球心0;另一条光线的入射点为A,穿过玻璃后两条光线交于P点.已知玻璃球的圆半径为R,OA=
(2013?太原一模)两束平行的细激光束,垂直于半球形玻璃体的圆平面射到半圆球体上,如图所示.已知其中一条光线沿直线穿过玻璃,它的入射点是球心0;另一条光线的入射点为A,穿过玻璃后两条光线交于P点.已知玻璃球的圆半径为R,OA=


