题目内容
 (2013?太原一模)两束平行的细激光束,垂直于半球形玻璃体的圆平面射到半圆球体上,如图所示.已知其中一条光线沿直线穿过玻璃,它的入射点是球心0;另一条光线的入射点为A,穿过玻璃后两条光线交于P点.已知玻璃球的圆半径为R,OA=
(2013?太原一模)两束平行的细激光束,垂直于半球形玻璃体的圆平面射到半圆球体上,如图所示.已知其中一条光线沿直线穿过玻璃,它的入射点是球心0;另一条光线的入射点为A,穿过玻璃后两条光线交于P点.已知玻璃球的圆半径为R,OA=| R |
| 2 |
| 3 |
(i)该玻璃的折射率;
(ii)光从A点传播到P点的时间.
分析:(i)光线沿直线从O点穿过玻璃,方向不变.从A点射入玻璃砖的光线方向不变,射到圆弧面上发生折射后射到P点,作出光路图,根据数学知识求出入射角和折射角,再由折射定律求出折射率.
(ii)根据数学知识求出光从A点传播到P点通过的路程s,光在玻璃内传播的速度v=
,在真空中速度为c,再根据t=
分别求出光在玻璃中和玻璃外的时间,再得到总时间.
(ii)根据数学知识求出光从A点传播到P点通过的路程s,光在玻璃内传播的速度v=
| c |
| n |
| s |
| v |
解答:解:(i)光线沿直线第一次到达圆弧面B点的入射角 θ1=30°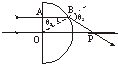
由几何关系可得:∠BOP=30°,所以折射角为 θ2=60°
玻璃的折射率
n=
=
=
(ii)光在玻璃内传播的速度
v=
=
光在玻璃内从A到B间的距离 L1=Rcos30°=
R
光在玻璃内传播的时间 t1=
=
=
,
BP间的距离 L2=R,
光从A点传播到P点的时间为
t2=
=
解得:t=t1+t2═
+
=
答:
(i)该玻璃的折射率为
;
(ii)光从A点传播到P点的时间为
.

由几何关系可得:∠BOP=30°,所以折射角为 θ2=60°
玻璃的折射率
n=
| sinθ2 |
| sinθ1 |
| sin60° |
| sin30° |
| 3 |
(ii)光在玻璃内传播的速度
v=
| c |
| n |
| c | ||
|
光在玻璃内从A到B间的距离 L1=Rcos30°=
| ||
| 2 |
光在玻璃内传播的时间 t1=
| L1 |
| v |
| ||||
|
| 3R |
| 2c |
BP间的距离 L2=R,
光从A点传播到P点的时间为
t2=
| L2 |
| c |
| R |
| c |
解得:t=t1+t2═
| 3R |
| 2c |
| R |
| c |
| 5R |
| 2c |
答:
(i)该玻璃的折射率为
| 3 |
(ii)光从A点传播到P点的时间为
| 5R |
| 2c |
点评:本题是几何光学问题,解题关键是作出光路图,根据几何知识求出入射角与折射角.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目

 (2013?太原一模)如图,一半径为R的圆表示一柱形区域的横截面(纸面).在柱形区域内加一方向垂直于纸面向外的匀强磁场,磁感应强度大小为B.一质量为m、电荷量为q的带正电粒子以某一初速度v0(未知)从a点沿直径aOb方向射入柱形区域(磁场),从圆上的C点离开该区域,已知Oc与Ob成60°角,回答下列问题:
(2013?太原一模)如图,一半径为R的圆表示一柱形区域的横截面(纸面).在柱形区域内加一方向垂直于纸面向外的匀强磁场,磁感应强度大小为B.一质量为m、电荷量为q的带正电粒子以某一初速度v0(未知)从a点沿直径aOb方向射入柱形区域(磁场),从圆上的C点离开该区域,已知Oc与Ob成60°角,回答下列问题: (2013?太原一模)如图所示.开口竖直向上的固定气缸内有一质量为m的活塞,在距气缸底部1.2L处有一个卡环,活塞可以在气缸内卡环以上部分无摩擦滑动但不漏气,一“U”形管气压计,左端连接在卡环与气缸底部之间.现在气缸内封闭一定质量的空气,当温度为T0活塞静止时距气缸底部为1.5L.已知水银的密度为ρ,大气压强恒为P0,气缸横截面积为s,不计“U”形管内气体的体积,求:
(2013?太原一模)如图所示.开口竖直向上的固定气缸内有一质量为m的活塞,在距气缸底部1.2L处有一个卡环,活塞可以在气缸内卡环以上部分无摩擦滑动但不漏气,一“U”形管气压计,左端连接在卡环与气缸底部之间.现在气缸内封闭一定质量的空气,当温度为T0活塞静止时距气缸底部为1.5L.已知水银的密度为ρ,大气压强恒为P0,气缸横截面积为s,不计“U”形管内气体的体积,求: