题目内容
1.如图所示,一半径r=0.2m的$\frac{1}{4}$光滑圆弧形槽底端B与水平传带相接,传送带的运行速度为v0=4m/s,长为L=1.25m,滑块与传送带间的动摩擦因数μ=0.2,DEF为固定于竖直平面内的一段内壁光滑的中空方形细管,EF段被弯成以O为圆心、半径R=0.25m的一小段圆弧,管的D端弯成与水平传带C端平滑相接,O点位于地面,OF 连线竖直.一质量为M=0.2kg的物块a从圆弧顶端A点无初速滑下,经过传送带,然后滑块被传送带送入管DEF,已知a可视为质点,a横截面略小于管中空部分的横截面,重力加速度g取10m/s2.求: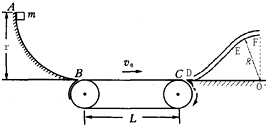
(1)滑块a到达底端B时的速度vB;
(2)滑块a刚到达管顶F点时对管壁的压力;
(3)滑块a滑到F点飞出后落地,求滑块a的落地点到O点的距离x(不计空气阻力).
分析 (1)滑块a从A下滑到B的过程中,支持力不做功,只有重力做功,机械能守恒,由机械能守恒定律求解速度vB;
(2)先研究滑块传送带上的运动过程,再研究滑块冲上细管的过程:滑块在传送带上做匀加速运动,根据牛顿第二定律和运动学公式结合求出滑块到达C点时的速度,滑块从C至F,由机械能守恒定律求出到达F点时的速度,由牛顿第二定律求出管道对滑块的弹力,由牛顿第三定律即可解得滑块在F点时对管壁的压力;
(3)滑块从F点飞出做平抛运动,运用运动的分解法求解滑块a的落地点到O点的距离x.
解答 解:(1)设滑块到达B点的速度为vB,由机械能守恒定律,有
Mgr=$\frac{1}{2}$MvB2.
解得 vB=2m/s
(2)滑块在传送带上做匀加速运动,受到传送带对它的滑动摩擦力,
由牛顿第二定律 μMg=Ma
滑块对地位移为L,末速度为vC,设滑块在传送带上一直加速
由速度位移关系式 2aL=vC2-vB2
代入数据解得vC=3m/s<4m/s,可知滑块未达共速
滑块从C至F,由机械能守恒定律,有 $\frac{1}{2}$MvC2=MgR+$\frac{1}{2}$MvF2
代入数据解得 vF=2m/s
在F处,由牛顿第二定律得
Mg+FN=M$\frac{{v}_{F}^{2}}{R}$
代入数据解得 FN=0.6N
根据牛顿第三定律知,管上壁受的压力为 FN′=FN=0.6N,方向竖直向上.
(3)滑块从F点飞出做平抛运动,得
x=vFt,
R=$\frac{1}{2}$gt2.
代入数据解得 x=$\frac{\sqrt{5}}{5}$m
答:
(1)滑块a到达底端B时的速度vB是2m/s.
(2)滑块a刚到达管顶F点时对管壁的压力是0.6N,方向竖直向上.
(3)滑块a滑到F点飞出后落地,滑块a的落地点到O点的距离x是$\frac{\sqrt{5}}{5}$m.
点评 本题按时间顺序进行分析,关键要把握每个过程所遵守的物理规律,运用机械能守恒、牛顿第二定律、运动学公式结合进行求解.

| A. | 单摆的质量越大,回复力越大,周期越短 | |
| B. | 单摆的摆长越长,往返一次所走过的路程越大,其周期越长 | |
| C. | 单摆周期不仅与摆长有关,还与单摆所处的地理位置有关 | |
| D. | 用单摆制成的座钟在北京走时准确,在搬到深圳后要走时仍准确,必须调整缩短单摆的摆长 |
 如图所示,两根平行电阻不计的金属导轨水平放置,间距为L,其间有竖直向下的匀强磁场,磁感应强度为B.垂直于轨道水平对称放置一根质量为m、电阻为R的金属棒,金属棒与导轨间的动摩擦因数为μ.从t=0时刻起,导轨左端连接一正弦交流电u=Umsinωt,金属棒始终保持静止状态,设最大静摩擦力等于滑动摩擦力,则( )
如图所示,两根平行电阻不计的金属导轨水平放置,间距为L,其间有竖直向下的匀强磁场,磁感应强度为B.垂直于轨道水平对称放置一根质量为m、电阻为R的金属棒,金属棒与导轨间的动摩擦因数为μ.从t=0时刻起,导轨左端连接一正弦交流电u=Umsinωt,金属棒始终保持静止状态,设最大静摩擦力等于滑动摩擦力,则( )| A. | 当t=$\frac{π}{2ω}$时,金属棒受到的安培力为零 | |
| B. | 当t=$\frac{2π}{ω}$时,金属棒受到的安培力大小为$\frac{B{U}_{m}L}{R}$ | |
| C. | 从t=0到t=$\frac{π}{ω}$的过程中,金属棒上产生的电热为$\frac{π{{U}_{m}}^{2}}{2Rω}$ | |
| D. | 交变电源电压的峰值Um≤$\frac{μmgR}{BL}$ |
 在X轴上的-L和L点分别固定了A,B两个点电荷,A的电荷量为+Q,B的电荷量为-Q,如图所示,设沿X轴正方向为电场强度的正方向,则整个X轴上的电场强度E随X变化的图象正确的是( )
在X轴上的-L和L点分别固定了A,B两个点电荷,A的电荷量为+Q,B的电荷量为-Q,如图所示,设沿X轴正方向为电场强度的正方向,则整个X轴上的电场强度E随X变化的图象正确的是( )| A. |  | B. |  | C. |  | D. |  |
 如图所示,带箭头的线段表示某一电场中的电场线的分布情况.一带电粒子在电场中运动的轨迹如图中虚线所示.只受电场力,则下列判断中正确的是( )
如图所示,带箭头的线段表示某一电场中的电场线的分布情况.一带电粒子在电场中运动的轨迹如图中虚线所示.只受电场力,则下列判断中正确的是( )| A. | 若粒子是从A运动到B,则粒子带正电;若粒子是从B运动到A,则粒子带负电 | |
| B. | 不论粒子是从A运动到B,还是从B运动到A,粒子必带正电 | |
| C. | 若粒子是从B运动到A,则其加速度增大 | |
| D. | 若粒子是从A运动到B,则电势能一定增大 |