题目内容
银河系的恒量中大约有四分之一是双星,某双星由质量不等的星体S1和S2构成,两星在相互之间的万有引力作用下绕两者连线某一点C做匀速圆周运动,已知S1和S2的质量分别为M1和M2,S1和S2的距离为L,已知引力常数为G.由此可求出S1的角速度为( )
A.
| B.
| C.
| D.
|
设星体S1和S2的质量分别为m1、m2,
星体S1做圆周运动的向心力由万有引力提供得:
=M1ω2r1…①
星体S2做圆周运动的向心力由万有引力提供得:
=M2ω2r2…②
M2①+M1②得:
M2
+M1
=M1M2ω 2(r1+r2),
r1+r2=L
即:ω=
,与B选项一致,故正确选项为B.
故选:B.
星体S1做圆周运动的向心力由万有引力提供得:
| GM1M2 |
| L2 |
星体S2做圆周运动的向心力由万有引力提供得:
| GM1M2 |
| L2 |
M2①+M1②得:
M2
| GM1M2 |
| L2 |
| GM1M2 |
| L2 |
r1+r2=L
即:ω=
|
故选:B.

练习册系列答案
相关题目
 (B)
(B)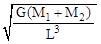 (C)
(C)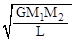 (D)
(D)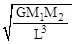
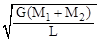 B.
B.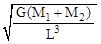 C.
C. D.
D.



