题目内容
如图所示,两块竖直放置的导体板间存在水平向左的匀强电场,板间距离为d.有一带电量为+q、质量为m的小球(可视为质点)以水平速度从A孔进入匀强电场,且恰好没有与右板相碰,小球最后从B孔离开匀强电场,若A、B两孔的距离为4d,重力加速度为g,求:
(1)两板间的场强大小;
(2)小球从A孔进入电场时的速度;
(3)从小球进入电场到其速度达到最小值,小球电势能的变化量为多少?
(1)两板间的场强大小;
(2)小球从A孔进入电场时的速度;
(3)从小球进入电场到其速度达到最小值,小球电势能的变化量为多少?

(1)由题意可知,小球在水平方向先减速到零,然后反向加速.设小球进入A孔的速度为v0,减速到右板的时间为t,则有:
水平方向:d=v0t-
t20=v0-
t
竖直方向:4d=
g(2t)2
联立解得E=
(2)在水平方向上根据牛顿第二定律有qE=max
根据运动学公式有0-
=2(-ax)d
联立解得v0=
(3)小球进入电场后,在水平方向上做减速运动,即vx=v0-
t′=v0-gt′
在竖直方向上做加速运动,即vy=gt'
小球在电场中的速度大小为v=
联立由数学知识可得t′=
时小球速度达到最小,最小值为
v0;
此时粒子在水平方向的位移为:x=v0t′-
t′2
在此过程中电场力做功为W=-qEx
而W=-△Ep
联立解得△Ep=
mgd,即粒子的电势能增加
mgd
答:(1)两板间的场强大小为
;
(2)小球从A孔进入电场时的速度为
;
(3)从小球进入电场到其速度达到最小值为
v0,小球电势能的增加量为
mgd.
水平方向:d=v0t-
| 1 |
| 2 |
| qE |
| m |
| qE |
| m |
竖直方向:4d=
| 1 |
| 2 |
联立解得E=
| mg |
| q |
(2)在水平方向上根据牛顿第二定律有qE=max
根据运动学公式有0-
| v | 20 |
联立解得v0=
| 2gd |
(3)小球进入电场后,在水平方向上做减速运动,即vx=v0-
| qE |
| m |
在竖直方向上做加速运动,即vy=gt'
小球在电场中的速度大小为v=
|
联立由数学知识可得t′=
| v0 |
| 2g |
| ||
| 2 |
此时粒子在水平方向的位移为:x=v0t′-
| 1 |
| 2 |
| qE |
| m |
在此过程中电场力做功为W=-qEx
而W=-△Ep
联立解得△Ep=
| 3 |
| 4 |
| 3 |
| 4 |
答:(1)两板间的场强大小为
| mg |
| q |
(2)小球从A孔进入电场时的速度为
| 2gd |
(3)从小球进入电场到其速度达到最小值为
| ||
| 2 |
| 3 |
| 4 |

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 (2013?怀化三模)如图所示,两块水平放置的金属板距离为d,用导线、电键K与一个n匝的线圈连接,线圈置于方向竖直向上的均匀变化的磁场中.两板间放一台小压力传感器,压力传感器上表面绝缘,在其上表面静止放置一个质量为m、电量为+q的小球.电键K闭合前传感器上有示数,电键K闭合后传感器上的示数变为原来的一半.则线圈中磁场的变化情况和磁通量变化率分别是( )
(2013?怀化三模)如图所示,两块水平放置的金属板距离为d,用导线、电键K与一个n匝的线圈连接,线圈置于方向竖直向上的均匀变化的磁场中.两板间放一台小压力传感器,压力传感器上表面绝缘,在其上表面静止放置一个质量为m、电量为+q的小球.电键K闭合前传感器上有示数,电键K闭合后传感器上的示数变为原来的一半.则线圈中磁场的变化情况和磁通量变化率分别是( ) (2011?永春县模拟)如图所示,两块水平放置的金属板距离为d,用导线、电键K与一个n匝的线圈连接,线圈置于方向竖直向上的均匀变化的磁场中.两板间放一台小压力传感器,压力传感器上表面绝缘,在其上表面静止放置一个质量为m、电量为+q的小球.电键K闭合前传感器上有示数,电键K闭合后传感器上的示数变为原来的一半,则线圈中磁场的变化情况和磁通量变化率分别是( )
(2011?永春县模拟)如图所示,两块水平放置的金属板距离为d,用导线、电键K与一个n匝的线圈连接,线圈置于方向竖直向上的均匀变化的磁场中.两板间放一台小压力传感器,压力传感器上表面绝缘,在其上表面静止放置一个质量为m、电量为+q的小球.电键K闭合前传感器上有示数,电键K闭合后传感器上的示数变为原来的一半,则线圈中磁场的变化情况和磁通量变化率分别是( )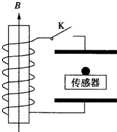 如图所示,两块水平放置的金属板距离为d,用导线、电键K与一个n匝的线圈连接,线圈置于方向竖直向上的均匀变化的磁场中.两板间放一台小压力传感器,压力传感器上表面绝缘,在其上表面静止放置一个质量为m,电量为+q的小球.电键K闭合前传感器上有示数,电键K闭合后传感器上的示数变为原来的2倍.则线圈中磁场的变化情况和磁通量变化率分别是( )
如图所示,两块水平放置的金属板距离为d,用导线、电键K与一个n匝的线圈连接,线圈置于方向竖直向上的均匀变化的磁场中.两板间放一台小压力传感器,压力传感器上表面绝缘,在其上表面静止放置一个质量为m,电量为+q的小球.电键K闭合前传感器上有示数,电键K闭合后传感器上的示数变为原来的2倍.则线圈中磁场的变化情况和磁通量变化率分别是( )
