题目内容

如图所示，两个摩擦传动而无相对滑动的轮子A、B，A为主动轮，半径是Rl，转动的角速度为ω；B轮的半径为R2，C点在B轮上，距圆心O2为
R2
2
，则vA：vC
=2：1
=2：1
，C点处的向心加速度是
ω2
R
2
1
 
2R2
ω2
R
2
1
 
2R2
m/s2．
分析：同缘传动边缘上的点线速度相等；同轴传动角速度相同；同时结合公式v=ωr和an=ω2R列式求解．
解答：解：A、B两轮子边缘上的点线速度大小相等，有：R1ω=R2ωB
解得ωB=
R1
R2
ω，
由于C点上的角速度与轮B的角速度相等，则：
C点的线速度vC=
R2
2
ωB=
1
2
R1ω
A点的线速度vA=ωR1
故AB两点的线速度之比vA：vC=2：1
C处的向心加速度a=
R2
2
ωB2=
ω2
R
2
1
 
2R2
．
故答案为：2：1，
ω2
R
2
1
 
2R2
．
点评：解决本题的关键是要知道共轴转动的点角速度大小相等，靠摩擦传动轮子边缘上的点线速度大小相等，掌握向心加速度与线速度和角速度的关系．
练习册系列答案
相关题目
如图所示，一平直的传送带以速率v=2m/s匀速运动，传送带与水平面夹角为θ=30°，传送带把A处的工件不断地运到较高的B处，A、B两处相距L=30m．从A处把工件轻轻地放到传送带上，经过时间t=20s能传到B处．假设A处每隔一定时间放上一工件，每小时恰好运送7200个工件，每个工件的质量为m=2kg，求：（g=10m/s2）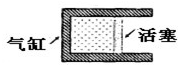
（1）工件加速运动的时间t0；
（2）工件加速时的加速度大小；
（3）不计轮轴处的摩擦，求带动传送带的电动机的平均输出功率．
精英家教网（1）下列说法正确的是
 

A．继续给打足气的篮球打气是很困难的，这是因为此时气体分子之间存在着斥力的缘故
B．甲、乙两系统有微观态分别为N个和2N个，那么自发进行方向是甲→乙
C．热量不能从低温的物体自发地传到高温的物体
D．能量守恒定律是自然界普遍规律，节能只是为“减排”和节约开支而言
（2）夏日里池塘底部经常会冒出气泡．若视气泡内的气体为一定质量的理想气体，在气泡缓慢上升过程中若温度保持不变，则
 

A．体积增大，吸收热量    B．体积减小，放出热量
C．体积增大，压强增大    D．气体对外做功，内能不变
（3）如图所示，水平放置的汽缸内用活塞封闭着一定质量的理想气体，初始状态气体的体积为V1、温度为T1．现对汽缸缓缓加热，使汽缸内的空气温度从T1升高到T2．已知外界大气压强恒为P0．不计活塞与气缸之间的摩擦．此过程中被封闭气体的体积是否发生变化？说说你的理由．若发生变化，则变化了多少？

“物理3－3”模块（10分）

（1）下列有关热学知识的论述正确的是 （     ）

A．教室内看到透过窗子的“阳光柱”里粉尘颗粒杂乱无章的运动，这种运动是布朗运动

B．只要知道水的摩尔质量和水分子的质量，就可以计算出阿伏伽德罗常数

C．在使两个分子间的距离由很远（r＞10-9m）减小到很难再靠近的过程中，分子间作用力先减小后增大；分子势能不断增大

D．温度是物体分子热运动平均动能的标志

E．两个温度不同的物体相互接触时，热量既能自发地从高温物体传给低温物体，也可以自发地从低温物体传给高温物体

F．熵是物体内分子运动无序程度的量度

（2）实验室内，某同学用导热性能良好的气缸和活塞将一定质量的理想气体密封在气缸内（活塞与气缸壁之间无摩擦），活塞的质量为m，气缸内部的横截面积为S．用滴管将水缓慢滴注在活塞上，最终水层的高度为h，如图所示．在此过程中，若大气压强恒为p0，室内的温度不变，水的密度为ρ，重力加速度为g，则以下图象中能反映密闭气体状态变化过程的是（     ）

 


（3）上题中若初始时，活塞离气缸底部的高度为H，则活塞下降的高度为多少？此过程中气缸内气体吸热还是放热，说明理由。

 【选做题】本题包括A、B、C三小题，请选定其中两题，并在答题卡相应的答题区域内作答．若三题都做，则按A、B两题评分．

A．(选修模块3—3)（12分）

（1）（4分）判断以下说法的正误，在相应的括号内打“√”或“×”。

  （A）用手捏面包，面包体积会缩小，说明分子之间有间隙。（    ）

  （B）温度相同的氢气和氧气，氢气分子和氧气分子的平均速率相同。（    ）

  （C）夏天荷叶上小水珠呈球状，是由于液体表面张力使其表面积具有收缩到最小趋势的缘故。（    ）

  （D）自然界中进行的一切与热现象有关的宏观过程都具有方向性。（    ）

（2）（4分）在“用油膜法估测分子的大小”的实验中，有下列操作步骤，请补充实验步骤的内容及实验步骤中的计算式：

  （A）用滴管将浓度为的油酸酒精溶液逐滴滴入量筒，记下的油酸酒精溶液的滴数；

  （B）将痱子粉末均匀地撒在浅盘内的水面上，用滴管吸取浓度为的油酸酒精溶液，逐滴向水面上滴入，直到油酸薄膜表面足够大，且不与器壁接触为止，记下滴入的滴数；

  （C）________________▲________________；

  （D）将画有油酸薄膜轮廓的玻璃板放在坐标纸上，以坐标纸上边长的正方形为单位，计算轮廓内正方形的个数；

  （E）用上述测量的物理量可以估算出单个油酸分子的直径__▲____。

（3）如图所示，上端开口的光滑圆柱形气缸竖直放置，截面积为40cm2的活塞将

一定质量的气体和一形状不规则的固体A封闭在气缸内。在气缸内距缸底60cm   

处设有卡环ab，使活塞只能向上滑动。开始时活塞搁在ab上，缸内气体的压

强等于大气压强为p0＝1.0×105Pa，温度为300K。现缓慢加热汽缸内气体，当

温度缓慢升高为330K，活塞恰好离开ab；当温度缓慢升高为360K时，活塞上

升了4cm。求：

（1）活塞的质量；

（2）整个过程中气体对外界做的功。

B．(选修模块3—4)（12分）

（1）（4分）判断以下说法的正误，在相应的括号内打“√”或“×”。

   （A）光速不变原理是狭义相对论的两个基本假设之一。（      ）

   （B）拍摄玻璃橱窗内的物品时，往往在镜头前加一个偏振片以增加透射光的强度。（      ）

   （C）光在介质中的速度大于光在真空中的速度。（      ）

（D）变化的电场一定产生变化的磁场；变化的磁场一定产生变化的电场。（      ）

   

（2）（4分）如图为一横波发生器的显示屏，可以显示出波由0点从左向右传播的图像，屏上每一小格长度为1cm。在t＝0时刻横波发生器上能显示的波形如图所示。因为显示屏的局部故障，造成从水平位置A到B之间（不包括A、B两处）的波形无法被观察到（故障不影响波在发生器内传播）。此后的时间内，观察者看到波形相继传经B、C处，在t＝5秒时，观察者看到C处恰好第三次（从C开始振动后算起）出现平衡位置，则该波的波速可能是

（A）3.6cm/s    （B）4.8cm/s

（C）6cm/s     （D）7.2cm/s

 

 

 

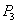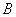（3）（4分）如图所示，某同学用插针法测定一半圆形玻璃砖的折射率。在平铺的白纸上垂直纸面插大头针、确定入射光线，并让入射光线过圆心，在玻璃砖（图中实线部分）另一侧垂直纸面插大头针，使挡住、的像，连接。图中为分界面，虚线半圆与玻璃砖对称，、分别是入射光线、折射光线与圆的交点，、均垂直于法线并分别交法线于、点。设的长度为，的长度为，的长度为，的长度为，求：

①为较方便地表示出玻璃砖的折射率，需用刻度尺测量（用上述给  

出量的字母表示），

②玻璃砖的折射率

 

 

C．(选修模块3—5)（12分）

（1）下列说法中正确的是___▲_____

（A）X射线是处于激发态的原子核辐射出的

（B）放射性元素发生一次β衰变，原子序数增加1

（C）光电效应揭示了光具有粒子性，康普顿效应揭示了光具有波动性

（D）原子核的半衰期不仅与核内部自身因素有关，还与原子所处的化学状态 

有关

（2）氢原子的能级如图所示，当氢原子从n=4向n=2的能级跃迁时，辐射的光  

子照射在某金属上，刚好能发生光电效应，则该金属的逸出功为 ▲  eV。

现有一群处于n=5的能级的氢原子向低能级跃迁，在辐射出的各种频率的

光子中，能使该金属发生光电效应的频率共有   ▲    种。

 

（3）如图，质量为m的小球系于长L＝0.8m的轻绳末端。绳的另一端

系于O点。将小球移到轻绳水平位置后释放，小球摆到最低点A

时，恰与原静止于水平面上的物块P相碰。碰后小球回摆，上升的

最高点为B，A、B的高度差为h＝0.2m。已知P的质量为M＝3m，

P与水平面间的动摩擦因数为μ＝0.25，小球与P的相互作用时间

极短。求P沿水平面滑行的距离。

 

 

 【选做题】本题包括A、B、C三小题，请选定其中两题，并在答题卡相应的答题区域内作答．若三题都做，则按A、B两题评分．

A．(选修模块3—3)（12分）

（1）在研究性学习的过程中，针对能源问题，大气污染问题同学们提出了如下四个活动方案，哪些从理论上讲是可行的

（A）发明一种制冷设备，使温度降至绝对零度以下

（B）汽车尾气中各类有害气体排入大气后严重污染了空气，想办法使它们自发地分离，既清洁了空气，又变废为宝

（C）某国际科研小组正在研制利用超导材料制成灯泡的灯丝和闭合电路．利用电磁感应激起电流后，由于电路电阻为零从而使灯泡一直发光

（D）由于太阳的照射，海洋表面的温度可达30℃左右，而海洋深处的温度要低得多，在水600～1000m的地方，水温约为4℃．据此，科学家研制了一种抗腐蚀的热交换器，利用海水温差发电

（2）秋天附着在树叶上的露水常呈球形，.这是因为____▲____．水银放在某一固体容器中，其液面向下弯，说明水银__▲___这种固体（填“浸润”或“ 不浸润”）．

（3）如图所示，在竖直放置绝热圆柱形容器内用质量为m的绝热活塞密封一部分气体，活塞与容器壁间能无摩擦滑动，容器的横截面积为S，开始时密闭气体的温度为T0，活塞与容器底的距离为h0．现将整个装置放在大气压恒为P0的空气中，当气体从外界吸收热量Q后，活塞缓慢上升d后再次平衡，问：

①此时密闭气体的温度是多少？

②在此过程中密闭气体的内能增加了多少？

B．(选修模块3—4)（12分）

（1）下列说法中正确的有    ▲   ．

（A）2010年4月14日早晨7时49分，青海省玉树藏族自治州玉树县发生7.1级地震，造成重大人员财产损失，地震波是机械波，地震波中既有横波也有纵波

（B）太阳能真空玻璃管采用镀膜技术增加透射光，这是利用了光的衍射原理

（C）相对论认为：真空中的光速在不同惯性参照系中是不相同的

（D）医院里用于检测的“彩超”的原理是：向病人体内发射超声波，经血  

液反射后被接收，测出反射波的频率变化，就可知血液的流速．这 

一技术应用了多普勒效应

（2）如图所示为一列简谐波在t1=0时刻的图象，此时波中质点M的运动方   

向沿y轴负方向，且到t2=0.55s质点M恰好第3次到达y轴正方向最大 

位移处，该波的传播方向为__▲___，波速为___▲____m／s．

（3）如图所示是一种折射率n=1.5的棱镜．现有一束光 线沿MN的方向射  

到棱镜的AB界面上，入射角的大小．求光在棱镜中传

播的速率及此束光线射出棱镜后的方向（不考虑返回到AB面上的光线）．

C．(选修模块3—5)（12分）

（1）下列说法中正确的有___▲____．

（A）黑体辐射时电磁波的强度按波长的分布只与黑体的温度有关

（B）普朗克为了解释光电效应的规律，提出了光子说

（C）天然放射现象的发现揭示原子核有复杂的结构

（D）卢瑟福首先发现了质子和中子

（2）如图所示是使用光电管的原理图．当频率为v的可见光照射到阴极K上时，  

电流表中有电流通过．

  ①当变阻器的滑动端P向    ▲    滑动时（填“左”或“右”），通过电流表的电流将会减小．

  ②当电流表电流刚减小到零时，电压表的读数为U，则光电子的最大初动能为

        ▲    （已知电子电荷量为e）．

  ③如果不改变入射光的频率，而增加入射光的强度，则光电子的最大初动能将__▲___

（填“增加”、“减小”或“不变”）．

（3）一炮弹质量为m，以一定的倾角斜向上发射，到达最高点时速度为v，炮弹在最高点爆炸成两块，

其中一块恰好做自由落体运动，质量为．则另一块爆炸后瞬时的速度大小__▲__。

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网