题目内容
16.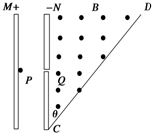 如图所示,M、N为两块带等量异种电荷的平行金属板,两板间电压可取从零到最大值Um之间的各种数值.静止的带电粒子电荷量为+q,质量为m(不计重力),从点P经电场加速后,从小孔Q进入N板右侧的匀强磁场区域,磁场方向垂直于纸面向外,CD为磁场边界上的一绝缘板,它与N板的夹角为θ=45°,孔Q到板的下端C的距离为L,当M、N两板间电压取最大值Um时,粒子恰垂直打在CD板上.求:
如图所示,M、N为两块带等量异种电荷的平行金属板,两板间电压可取从零到最大值Um之间的各种数值.静止的带电粒子电荷量为+q,质量为m(不计重力),从点P经电场加速后,从小孔Q进入N板右侧的匀强磁场区域,磁场方向垂直于纸面向外,CD为磁场边界上的一绝缘板,它与N板的夹角为θ=45°,孔Q到板的下端C的距离为L,当M、N两板间电压取最大值Um时,粒子恰垂直打在CD板上.求:(1)当M、N两板间电压取最大值Um时,粒子射入磁场的速度v1的大小;
(2)匀强磁场的磁感应强度B的大小;
(3)粒子在磁场中运动的最长时间tm;
(4)CD板上可能被粒子打中区域的长度S.
分析 带电粒子在带等量异种电荷的电场在加速,离开电场进入匀强磁场做匀速圆周运动,由于进入磁场的速度不同,半径也不相等,本题涉及的几种特殊情况.
(1)由动能定理,电场力做的功就是粒子动能的增加量,从而求出速度的射入磁场的速度.
(2)由垂直打在板上知道速度方向,从而求出半径,由洛仑兹力提供向心力就可求出此种情况下磁感应强度的大小.
(3)显然在磁场中做完整的半周的时间就是最长时间.
(4)由分析知:最大速度的位置打在CD板上离C点最远,与CD相切的位置最近.两者之差就是打在CD板上的长度.
解答 解:(1)M、N两板间电压取最大值Um时,粒子恰垂直打在CD板上,所以圆心在C点,如图所示,设此时粒子
运动轨迹半径为r1,CH=QC=L 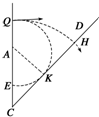
即半径r1=L
由qUm=$\frac{1}{2}m{{v}_{1}}^{2}$ ${v}_{1}=\sqrt{\frac{2q{U}_{m}}{m}}$
(2)又因为qv1B=m $\frac{{{v}_{1}}^{2}}{{r}_{1}}$
得B=$\sqrt{\frac{2m{U}_{m}}{q{L}^{2}}}$
(3)打在QE间的粒子在磁场中运动的时间最长,均为半个周期,
由$T=\frac{2πr}{v}=\frac{2πm}{qB}$而 ${t}_{m}=\frac{T}{2}$
得tm=$πL\sqrt{\frac{m}{2q{U}_{m}}}$
(4)设粒子在磁场中运动的轨迹与CD板相切于K点,此轨迹的半径为r2,设圆心为A,在△AKC中:sin 45°=$\frac{{r}_{2}}{L-{r}_{2}}$
解得r2=($\sqrt{2}$-1)L,
由几何关系:KC=r2=($\sqrt{2}$-1)L
所以CD板上可能被粒子打中的区域的长度s=HK=HC-KC,
即s=r1-r2=(2-$\sqrt{2}$)L
答:(1)当M、N两板间电压取最大值Um时,粒子射入磁场的速度v1的大小$\sqrt{\frac{2q{U}_{m}}{m}}$.
(2)匀强磁场的磁感应强度B的大小$\sqrt{\frac{2m{U}_{m}}{q{L}^{2}}}$.
(3)粒子在磁场中运动的最长时间为$πL\sqrt{\frac{m}{2q{U}_{m}}}$
(4)CD板上可能被粒子打中区域的长度S 为(2-$\sqrt{2}$)L.
点评 由洛仑兹力提供向心力可求得半径公式,从半径公式可以看出速度越大,半径越大,打的位置越上,由题意,找到几种特殊情况,从而能够求出速度、磁感应强度、最长时间等.

 名校课堂系列答案
名校课堂系列答案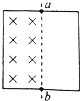 如图所示,用均匀导线做成边长为1m的正方形线框,线框的一半处于垂直线框向里的有界匀强磁场中,当磁场以0.2T/s的变化率增强时,a、b两点的电势分别为φa、φb,回路中电动势为E,则( )
如图所示,用均匀导线做成边长为1m的正方形线框,线框的一半处于垂直线框向里的有界匀强磁场中,当磁场以0.2T/s的变化率增强时,a、b两点的电势分别为φa、φb,回路中电动势为E,则( )| A. | φa<φb,E=0.2V | B. | φa>φb,E=0.2V | C. | φa<φb,E=0.1V | D. | φa>φb,E=0.1V |

| A. | I1>I2 | B. | I4<I2 | C. | U2=U3 | D. | U1>U2 |
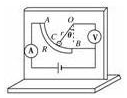 某同学设计了一个测定列车加速度的仪器,如图所示.AB是一段四分之一圆弧形的电阻,O点为其圆心,且在B点正上方,圆弧半径为r.O点下用一电阻不计的金属线悬挂着一个金属球,球的下部恰好与AB良好接触且无摩.A、B之间接有内阻不计、电动势为9V的电池,电路中接有理想电流表A,O、B间接有一个理想电压表V.整个装置在一竖直平面内,且装置所在平面与列车前进的方向平行.下列说法中正确的有( )
某同学设计了一个测定列车加速度的仪器,如图所示.AB是一段四分之一圆弧形的电阻,O点为其圆心,且在B点正上方,圆弧半径为r.O点下用一电阻不计的金属线悬挂着一个金属球,球的下部恰好与AB良好接触且无摩.A、B之间接有内阻不计、电动势为9V的电池,电路中接有理想电流表A,O、B间接有一个理想电压表V.整个装置在一竖直平面内,且装置所在平面与列车前进的方向平行.下列说法中正确的有( )| A. | 从图中看到列车可能是向左减速运动 | |
| B. | 当列车的加速度增大时,电流表A的读数增大,电压表V的读数也增大 | |
| C. | 若电压表显示3 V,则列车的加速度为$\frac{\sqrt{3}}{3}$g | |
| D. | 如果根据电压表示数与列车加速度的一一对应关系将电压表改制成一个加速度表,则加速度表的刻度是不均匀的 |
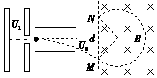 如图7所示,某种带电粒子由静止开始经电压为U1的电场加速后,射入水平放置、电势差为U2的两块导体板间的匀强电场中,带电粒子沿平行于两板的方向从两板正中间射入,穿过两板后又垂直于磁场方向射入边界线竖直的匀强磁场中,则粒子射入磁场和射出磁场的M、N两点间的距离d随着U1或U2的变化情况为(不计重力,不考虑边缘效应)( )
如图7所示,某种带电粒子由静止开始经电压为U1的电场加速后,射入水平放置、电势差为U2的两块导体板间的匀强电场中,带电粒子沿平行于两板的方向从两板正中间射入,穿过两板后又垂直于磁场方向射入边界线竖直的匀强磁场中,则粒子射入磁场和射出磁场的M、N两点间的距离d随着U1或U2的变化情况为(不计重力,不考虑边缘效应)( )| A. | d与U1无关,d随U2增大而增大 | B. | d与U2无关,d随U1增大而增大 | ||
| C. | d与U1无关,d随U2增大而减小 | D. | d与U2无关,d随U1增大而减小 |
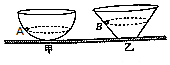 如图所示,甲表示小球A在半球形容器中做匀速圆周运动,乙表示小球B在一个圆锥形容器中做匀速圆周运动.不考虑两球在运动过程中的阻力.如果A、B的线速度均增大,下列关于两球运动角速度的说法正确的是( )
如图所示,甲表示小球A在半球形容器中做匀速圆周运动,乙表示小球B在一个圆锥形容器中做匀速圆周运动.不考虑两球在运动过程中的阻力.如果A、B的线速度均增大,下列关于两球运动角速度的说法正确的是( )| A. | A的增大、B的也增大 | B. | A的增大、B的减小 | ||
| C. | A的减小、B的增大 | D. | A的减小、B的也减小 |
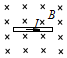 如图所示,一通电直导线位于匀强磁场中,导线与磁场方向垂直.当导线中的电流为I时,通电导线所受安培力的大小为F.当该导线中的电流变为2I时,保持其他条件不变,通电导线所受安培力的大小为( )
如图所示,一通电直导线位于匀强磁场中,导线与磁场方向垂直.当导线中的电流为I时,通电导线所受安培力的大小为F.当该导线中的电流变为2I时,保持其他条件不变,通电导线所受安培力的大小为( )| A. | $\frac{F}{2}$ | B. | F | C. | 2F | D. | 4F |
 如图所示,一长木板置于粗糙水平地面上,木板左端放置一小物块,木板的质量4kg,小物块质量1kg,可视为质点;小物块与木板间的动摩擦因数μ1=0.6,木板与地面间的动摩擦因数μ2=0.1,g=10m/s2;现对小物块施加水平推力F
如图所示,一长木板置于粗糙水平地面上,木板左端放置一小物块,木板的质量4kg,小物块质量1kg,可视为质点;小物块与木板间的动摩擦因数μ1=0.6,木板与地面间的动摩擦因数μ2=0.1,g=10m/s2;现对小物块施加水平推力F 如图所示,在平面坐标系xOy中,x≤0区域有垂直于y轴的匀强电场E=0.4N/C,x>0有三个区域Ⅰ、Ⅱ、Ⅲ,区域边界垂直于x轴,区域I的宽度L1=0.05m,区域Ⅱ的宽度L2=0.1m,区域Ⅲ的宽度L3未知,三个区域都有匀强磁场,磁感应强度大小相等都为B=0.02T,Ⅰ、Ⅲ中磁场方向垂直于坐标平面向外,Ⅱ中磁场方向垂直于坐标平面向里;P点在y轴上,纵坐标yP=0.15m,A点与P点纵坐标相等,与P点的距离d=1.0m.一正点电荷从A点由静止开始运动经过P点进入区域I,并从区域Ⅱ、Ⅲ之间边界上的C点(图中未标出)进入区域Ⅲ.点电荷质量m=2×10-9kg,电荷量q=4×10-4C,不计重力.
如图所示,在平面坐标系xOy中,x≤0区域有垂直于y轴的匀强电场E=0.4N/C,x>0有三个区域Ⅰ、Ⅱ、Ⅲ,区域边界垂直于x轴,区域I的宽度L1=0.05m,区域Ⅱ的宽度L2=0.1m,区域Ⅲ的宽度L3未知,三个区域都有匀强磁场,磁感应强度大小相等都为B=0.02T,Ⅰ、Ⅲ中磁场方向垂直于坐标平面向外,Ⅱ中磁场方向垂直于坐标平面向里;P点在y轴上,纵坐标yP=0.15m,A点与P点纵坐标相等,与P点的距离d=1.0m.一正点电荷从A点由静止开始运动经过P点进入区域I,并从区域Ⅱ、Ⅲ之间边界上的C点(图中未标出)进入区域Ⅲ.点电荷质量m=2×10-9kg,电荷量q=4×10-4C,不计重力.