题目内容
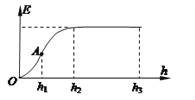
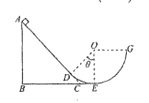
【题目】如图所示,斜面![]() 竖直固定放置,斜边
竖直固定放置,斜边![]() 与一光滑的圆弧轨道
与一光滑的圆弧轨道![]() 相切,切点为
相切,切点为![]() ,
,![]() 长为
长为![]() ,圆弧轨道圆心为
,圆弧轨道圆心为![]() ,半径为
,半径为![]() ,
,![]() ,
,![]() ,
,![]() 水平。现有一质量为
水平。现有一质量为![]() 、可视为质点的滑块从
、可视为质点的滑块从![]() 点由静止下滑,滑块与斜面间的动摩擦因数为
点由静止下滑,滑块与斜面间的动摩擦因数为![]() ,重力加速度为
,重力加速度为![]() ,则关于滑块的运动,下列说法正确的是( )
,则关于滑块的运动,下列说法正确的是( )
A. 滑块经过![]() 点时对轨道的最小压力为
点时对轨道的最小压力为![]()
B. 滑块下滑后将会从![]() 点飞出
点飞出
C. 滑块第二次经过![]() 点时对轨道的压力大小为
点时对轨道的压力大小为![]()
D. 滑块在斜面上经过的总路程为![]()
【答案】CD
【解析】
A、滑块从A点下滑后在AD部分轨道上要克服摩擦力做功,则返回到AD斜面上时的高度逐渐降低,最终滑块将在以E点为最低点、D为最高点来回滚动,此时经过E点时对轨道的压力最小,则D到E点,根据机械能守恒定律:![]() ,在E点:
,在E点:![]() ,联立解得:
,联立解得:![]() ,故A错误;
,故A错误;
B、从A到G由动能定理得:![]() ,其中
,其中![]() ,解得:
,解得:![]() ,则滑块下滑后不能从G点飞出,故B错误;
,则滑块下滑后不能从G点飞出,故B错误;
C、滑块第一次到达E点时,根据动能定理:![]() ,解得
,解得![]() ,第二次到达E点的速度与第一次相同,根据牛顿第二定律
,第二次到达E点的速度与第一次相同,根据牛顿第二定律![]() ,解得
,解得![]() ,故C正确;
,故C正确;
D、滑块最终将在以E点为最低点、D为最高点来回运动,根据动能定理:![]() ,解得
,解得![]() ,故D正确。
,故D正确。
故选CD。

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目