题目内容
如图所示，光滑斜面倾角为37°，一带有正电的小物块质量为m，电荷量为q，置于斜面上，当沿水平方向加有如图所示的匀强电场时，带电小物块恰好静止在斜面上，从某时刻开始，电场强度变化为原来的
，求：（1）原来的电场强度的大小；
（2）物体运动的加速度；
（3）沿斜面下滑距离为L时物体的速度的大小（sin37°=0.6，cos37°=0.8）
【答案】分析：（1）对小球进行受力分析，应用平衡条件可求出电场力，进而求出电场强度．
（2）电场变化后受力分析求出合外力应用牛顿第二定律求解加速度．
（3）沿斜面下滑距离为L时物体的速度的大小可由动能定理或运动学知识求解．
解答：解：（1）对小球受力分析并合成如图：
由平衡条件得：
F′=mg
在直角三角形中：
tanθ=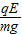
得：qE=mgtanθ，解得：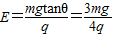
（2）对小球受力分析并正交分解如图：
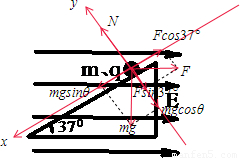
F合=mgsin37°-Fcos37°=ma
即：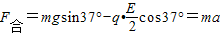
解得：a=3m/s2
方向：沿斜在向下
（3）在下滑过程中：W=F合×L
由动能定理：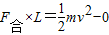
解得：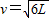
答：（1）原来的电场强度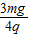
（2）物体运动的加速度为：a=3m/s2 方向：沿斜在向下
（3）沿斜面下滑距离为L时物体的速度的大小为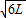
点评：问题一是平衡条件的应用，受力分析后应用平衡条件即可；问题二是牛顿运动定律的应用，关键是求合力；问题三直接应用动能定理即可，总体难度不是很大，细细分析即可．
（2）电场变化后受力分析求出合外力应用牛顿第二定律求解加速度．
（3）沿斜面下滑距离为L时物体的速度的大小可由动能定理或运动学知识求解．
解答：解：（1）对小球受力分析并合成如图：
由平衡条件得：
F′=mg
在直角三角形中：
tanθ=
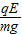
得：qE=mgtanθ，解得：
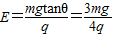
（2）对小球受力分析并正交分解如图：
F合=mgsin37°-Fcos37°=ma
即：
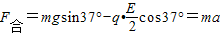
解得：a=3m/s2
方向：沿斜在向下
（3）在下滑过程中：W=F合×L
由动能定理：
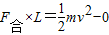
解得：
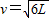
答：（1）原来的电场强度
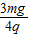
（2）物体运动的加速度为：a=3m/s2 方向：沿斜在向下
（3）沿斜面下滑距离为L时物体的速度的大小为
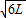
点评：问题一是平衡条件的应用，受力分析后应用平衡条件即可；问题二是牛顿运动定律的应用，关键是求合力；问题三直接应用动能定理即可，总体难度不是很大，细细分析即可．
练习册系列答案
相关题目
如图所示，一个质量分布均匀的球放在互成120°的两块光滑平面上保持静止状态OA是水平面，OB是倾斜面，关于球的受力，下列说法正确的是（ ）
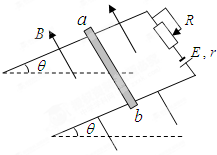如图所示，在倾θ=30°的绝缘斜面上，固定一L=0.25m的平行金属导轨，在导轨上端接入电源和滑动变阻器，电源电动E=12V，内r=1Ω，一质m=20g的金属ab与两导轨垂直并接触良好，整个装置处于磁感应强B=0.8T，方向垂直于斜面向上的匀强磁场中．金属导轨光滑，导轨与金属棒的电阻不计，g=10m/s2，要保持金属棒在导轨上静止，求：
如图所示，粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接，斜面倾a=37°，A、B、C是三个小滑块（可看做质点），A、B的质量均为m=1kg，B的左端附有胶泥（质量不计），C的质量均为M=2kg，D为两端分别连接B和C的轻质弹簧．
