题目内容
长度为L的细绳，一端系有一个质量为m的小球，另一端固定于O点，小球以O点为圆心在竖直平面内做圆周运动．设重力加速度为g．当小球刚好通过最高点时的速率v=
；若小球通过最高点时的速率为
，则在最高点细绳对小球的作用力大小F=
| gL |
| gL |
| 3gL |
2mg
2mg
．分析：小球刚好通过最高点时，绳子的拉力恰好为零，根据重力提供向心力，通过牛顿第二定律求出小球经过最高点的速率．小球通过最高点时的速率为
，小球受到重力和拉力的合力提供向心力，根据牛顿第二定律求出细绳对小球的作用力大小．
| 3gL |
解答：解：小球刚好通过最高点时，绳子的拉力恰好为零，有：mg=m
．
解得v=
．
小球通过最高点时的速率为
，有：F+mg=m
解得F=m
-mg=2mg．
故答案为：
，2mg．
| v2 |
| L |
解得v=
| gL |
小球通过最高点时的速率为
| 3gL |
| v′2 |
| L |
解得F=m
| v′2 |
| L |
故答案为：
| gL |
点评：解决本题的关键搞清小球做圆周运动的向心力的来源，运用牛顿第二定律进行求解．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
，求在最高点细绳对小球的作用力大小F。
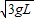，则在最高点细绳对小球的作用力大小F= ．