Question

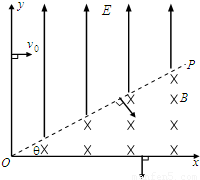
如图所示，POy区域内有沿y轴正方向的匀强电场，POx区域内有垂直纸面向里的匀强磁场，OP与x轴成θ角．不计重力的负电荷，质量为m、电量为q，从y轴上某点以初速度v₀垂直电场方向进入场区，经电场偏转后垂直OP进入磁场，然后又垂直x轴离开磁场．求：
（1）电荷进入磁场时的速度大小．
（2）电场力对电荷做的功．
（3）电场强度E与磁感应强度B的比值．

Answer 1

分析：（1）由运动的分解，即可求解；
（2）由动能定理，则可求出电场力做功；
（3）由牛顿第二定律，根据几何关系与速度的分解，则可求出电场强度与磁感应强度的比值．

解答：解：（1）设带电粒子到达OP进入磁场前的瞬时速度为v，则有：v=

v0

sinθ

（2）由动能定理，电场力做功为：WE=

1

2

mv2-

1

2

m

v

2 0

=

1

2

m

v

2 0

cot2θ
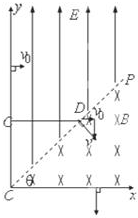
（3）设带电粒子在磁场中运动的半径为R，由牛顿第二定律：qvB=m

v2

R

依题意：

.

OD

=R  几何关系：

.

CD

=

.

OD

cosθ  有：

.

CD

=v0t  又，v_Dy=v₀cotθ  在 y 方向：vDy=

qE

m

t 
联立可得：

E

B

=v0
答：（1）电荷进入磁场时的速度大小为

v0

sinθ

．
（2）电场力对电荷做的功为

1

2

m

v

2 0

cot2θ．
（3）电场强度E与磁感应强度B的比值为v₀．

点评：考查运动的分解、动能定理、牛顿第二定律理解与掌握，同时结合几何关系来综合解题．