题目内容
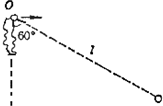 如图,长为L的轻绳一端系于固定点O,另一端系质量为m的小球.将小球从O点以一定初速水平向右抛出,经一定时间绳被拉直,以后小球将以O为支点在竖直平面内摆动.已知绳刚被拉直时,绳与竖直线成60度角,求:
如图,长为L的轻绳一端系于固定点O,另一端系质量为m的小球.将小球从O点以一定初速水平向右抛出,经一定时间绳被拉直,以后小球将以O为支点在竖直平面内摆动.已知绳刚被拉直时,绳与竖直线成60度角,求:(1)小球水平抛出时的初速v0
(2)小球摆到最低点时,绳所受的拉力T.
分析:(1)平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据高度求出时间,再根据水平位移和时间求出平抛运动的初速度.
(2)当绳子拉直后,沿绳子方向上的速度变为零,只剩下垂直于绳子方向上的分速度,根据机械能守恒定律求出小球摆动最低点的速度,再根据牛顿第二定律求出绳子的拉力.
(2)当绳子拉直后,沿绳子方向上的速度变为零,只剩下垂直于绳子方向上的分速度,根据机械能守恒定律求出小球摆动最低点的速度,再根据牛顿第二定律求出绳子的拉力.
解答:解:(1)根据L sin60°=V0t.
L cos60°=
gt2,
联立两式解得:t=
,v0=
.
(2)绳子拉直时,小球在竖直方向上的分速度vy=gt=
.
绳子拉直后,沿绳子方向上的速度变为零,只剩下垂直于绳子方向上的分速度,根据分解得:
v1=vysin60°-v0sin30°=
根据机械能守恒定律得:
mv22=
mv12+mgL(1-cos60°)
根据牛顿第二定律得:
F-mg=m
联立解得F=
mg.
答:(1)小球水平抛出时的初速度为v0=
.
(2)小球摆到最低点时,绳所受的拉力为
mg.
L cos60°=
| 1 |
| 2 |
联立两式解得:t=
|
| ||
| 2 |
(2)绳子拉直时,小球在竖直方向上的分速度vy=gt=
| gL |
绳子拉直后,沿绳子方向上的速度变为零,只剩下垂直于绳子方向上的分速度,根据分解得:
v1=vysin60°-v0sin30°=
| ||
| 4 |
根据机械能守恒定律得:
| 1 |
| 2 |
| 1 |
| 2 |
根据牛顿第二定律得:
F-mg=m
| v22 |
| L |
联立解得F=
| 35 |
| 16 |
答:(1)小球水平抛出时的初速度为v0=
| ||
| 2 |
(2)小球摆到最低点时,绳所受的拉力为
| 35 |
| 16 |
点评:本题综合考查了平抛运动和圆周运动,关键掌握平抛运动在水平方向和竖直方向上的运动规律,以及能够熟练运用牛顿第二定律和机械能守恒定律.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 如图所示,手持一根长为l的轻绳的一端在水平桌面上做半径为r、角速度为ω的匀速圆周运动,绳始终保持与该圆周相切,绳的另一端系一质量为m的木块,木块也在桌面上做匀速圆周运动,不计空气阻力,下列判断中正确的是( )
如图所示,手持一根长为l的轻绳的一端在水平桌面上做半径为r、角速度为ω的匀速圆周运动,绳始终保持与该圆周相切,绳的另一端系一质量为m的木块,木块也在桌面上做匀速圆周运动,不计空气阻力,下列判断中正确的是( )| A、手对木块的拉力做了功 | ||
| B、木块不受桌面的摩擦力 | ||
C、绳的拉力大小等于
| ||
D、手拉木块做功的功率等于
|
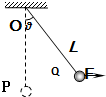 (2006?淮北模拟)一质量为m的小球,用长为L的轻绳悬挂于O点,小球 在水平力F作用下,从平衡位置P很缓慢地移动到Q点,如图所示,则力F所做的功为( )
(2006?淮北模拟)一质量为m的小球,用长为L的轻绳悬挂于O点,小球 在水平力F作用下,从平衡位置P很缓慢地移动到Q点,如图所示,则力F所做的功为( ) 一质量为m的小球,用长为L的轻绳悬挂在 O点,小球在水平恒力F作用下,从静止开始由平衡位置P点移动到Q点,此时绳与竖直方向的偏角为θ如图所示,则力F所做的功为( )
一质量为m的小球,用长为L的轻绳悬挂在 O点,小球在水平恒力F作用下,从静止开始由平衡位置P点移动到Q点,此时绳与竖直方向的偏角为θ如图所示,则力F所做的功为( ) (2012?房山区模拟)一质量为m的小球,用长为l的轻绳悬挂于O点,小球在水平拉力F作用下,从平衡位置P点由静止迅速拉到Q点,并使其获得速率v,如图所示,则力F所做的功为( )
(2012?房山区模拟)一质量为m的小球,用长为l的轻绳悬挂于O点,小球在水平拉力F作用下,从平衡位置P点由静止迅速拉到Q点,并使其获得速率v,如图所示,则力F所做的功为( ) 一质量为m的小球,用长为L的轻绳悬挂于O点,小球在水平力F作用下,从平衡位置P点很缓慢地移动到Q点,如图所示.则水平力F所做的功为
一质量为m的小球,用长为L的轻绳悬挂于O点,小球在水平力F作用下,从平衡位置P点很缓慢地移动到Q点,如图所示.则水平力F所做的功为