题目内容
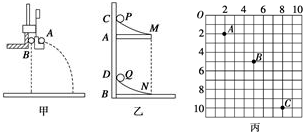
4.某同学用图1所示装置探究A、B两球在碰撞中动量是否守恒.该同学利用平抛运动测量两球碰撞前后的速度,实验装置和具体做法如下,图中PQ是斜槽,QR为水平槽.实验时先使A球从斜槽上某一固定位置G由静止开始滑下,落到位于水平地面的记录纸上,留下痕迹.重复上述操作10次,得到10个落点痕迹.再把B球放在水平槽上靠近槽末端的地方,让A球仍从位置G由静止开始滑下,和B球碰撞后,A、B球分别在记录纸上留下各自的落点痕迹.重复这种操作10次,并画出实验中A、B两小球落点的平均位置.图中O点是水平槽末端R在记录纸上的垂直投影点.其中米尺水平放置,且平行于G、R、O所在的竖直平面,米尺的零点与O点对齐.
(1)在以下选项中,哪些是本次实验必须进行的测量?AB
A.水平槽上未放B球时,测量A球落点位置到O点的距离
B.A球与B球碰撞后,测量A球与B球落点位置到O点的距离
C.A球和B球在空间飞行的时间
D.测量G点相对于水平槽面的高度
(2)如图2,E、F、J是实验中小球落点的平均位置,请你根据该同学实验的记录数据进行计算并判断,若实验中A、B两球碰撞中动量守恒,则mA:mB=2:1,两小球的碰撞是(选填“是”或“不是”)弹性碰撞.
分析 (1)根据实验的原理确定需要测量的物理量.
(2)根据碰撞前后小球的速度大小确定落点的位置.根据动量守恒列出表达式.再根据弹性碰撞的条件可明确是否为弹性碰撞.
解答 解:(1)根据动量守恒有:mAv0=mAv1+mBv2,因为v0=$\frac{{x}_{1}}{t}$,v1=$\frac{{x}_{2}}{t}$,v2=$\frac{{x}_{3}}{t}$.因为时间相同,可以用水平位移代替速度,所以需要测量水平槽上未放B球时,A球落点位置到O点的距离,A球与B球碰撞后,A球与B球落点位置到O点的距离.故A、B正确.
故选:AB.
(3)A球与B球碰后,A球的速度减小,可知A球没有碰撞B球时的落点是F点,A球与B球碰撞后A球的落点是E点.用水平位移代替速度,动量守恒的表达式为:
mAOF=mAOE+mBOJ.
由图可知OF=45cm;OE=15cm; OJ=60cm;
代入可得:mA:mB=2:1;
根据能量守恒可知,若是弹性碰撞,则应满足机械能守恒;代入数据可知:$\frac{1}{2}$mAOF2=$\frac{1}{2}$mAOE2+$\frac{1}{2}$mBOJ2.
故说明碰撞为弹性碰撞;
故答案为:(1)AB;(2)2:1; 是
点评 本题关键明确验证动量守恒定律实验的实验原理,注意等效替代在实验中的运用;同时注意根据速度公式分析对应的验证表达式.

练习册系列答案
相关题目
14. 如图所示,两轮用皮带转动,皮带不打滑,图中有A、B、C三点,这三点所在处的半径rA>rB=rC,则以下有关各点线速度v、加速度ω的关系中正确的是( )
如图所示,两轮用皮带转动,皮带不打滑,图中有A、B、C三点,这三点所在处的半径rA>rB=rC,则以下有关各点线速度v、加速度ω的关系中正确的是( )
 如图所示,两轮用皮带转动,皮带不打滑,图中有A、B、C三点,这三点所在处的半径rA>rB=rC,则以下有关各点线速度v、加速度ω的关系中正确的是( )
如图所示,两轮用皮带转动,皮带不打滑,图中有A、B、C三点,这三点所在处的半径rA>rB=rC,则以下有关各点线速度v、加速度ω的关系中正确的是( )| A. | vA=vB>vC | B. | vc>vA=vB | C. | ωc<ωA<ωB | D. | ωC=ωB>ωA |
15.关于简谐运动,以下说法正确的是( )
| A. | 物体做简谐运动时,系统的机械能一定不守恒 | |
| B. | 简谐运动是非匀变速运动 | |
| C. | 物体做简谐运动的回复力一定是由合力提供的 | |
| D. | 秒摆的周期正好是1s |
19.2011年3月11日,日本发生里氏九级大地震,造成福岛核电站的核泄漏事故.在泄露的污染物中含有131I和137Cs两种放射性元素,它们通过一系列衰变产生对人体有危害的辐射,其中131I的衰变方程为${\;}_{53}^{131}$I→${\;}_{54}^{131}$Xe+${\;}_{-1}^{0}$e,其半衰变期为8天.下列说法错误的是( )
| A. | 该核反应的实质是131I原子核内一个中子转变成了一个质子和一个电子 | |
| B. | ${\;}_{53}^{131}$I 原子核中含有78个中子 | |
| C. | 16个${\;}_{53}^{131}$I原子核经过16天有12个发生了衰变 | |
| D. | 已知该反应中生成的原子核${\;}_{54}^{131}$Xe处于高能级,则其在向低能级跃迁过程中可能释放γ光子 |
9. 已知均匀带电球壳内部电场强度处处为零,电势处处相等.如图所示,正电荷均匀分布在半球面上,Ox为通过半球顶点与球心O的轴线.A、B为轴上的点,且OA=OB.则下列判断正确的是( )
已知均匀带电球壳内部电场强度处处为零,电势处处相等.如图所示,正电荷均匀分布在半球面上,Ox为通过半球顶点与球心O的轴线.A、B为轴上的点,且OA=OB.则下列判断正确的是( )
 已知均匀带电球壳内部电场强度处处为零,电势处处相等.如图所示,正电荷均匀分布在半球面上,Ox为通过半球顶点与球心O的轴线.A、B为轴上的点,且OA=OB.则下列判断正确的是( )
已知均匀带电球壳内部电场强度处处为零,电势处处相等.如图所示,正电荷均匀分布在半球面上,Ox为通过半球顶点与球心O的轴线.A、B为轴上的点,且OA=OB.则下列判断正确的是( )| A. | A点的电场强度与B点的电场强度相同 | |
| B. | A点的电势等于B点的电势 | |
| C. | 在A点由静止开始释放重力不计的带正电粒子,该粒子将做匀加速直线运动 | |
| D. | 带正电的粒子在O点的电势能为零 |
13.灯泡是由谁发明的( )
| A. | 爱迪生 | B. | 普朗克 | C. | 牛顿 | D. | 伽利略 |

 如图所示,电场中同一条电场线上有A、B两点,A、B两点的电势差UAB=100V,将电荷量q=5.0×10-9 C的正点电荷从A点移到B点,求:
如图所示,电场中同一条电场线上有A、B两点,A、B两点的电势差UAB=100V,将电荷量q=5.0×10-9 C的正点电荷从A点移到B点,求: