题目内容
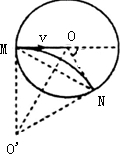
一匀强磁场分布在以O为圆心，半径为R的圆形区域内，方向与纸面垂直，如图所示，质量为m、电荷量q的带正电的质点，经电场加速后，以速度v沿半径MO方向进入磁场，沿圆弧运动到N点，然后离开磁场，∠MON=120°，质点所受重力不计，求：（1）判断磁场的方向；
（2）该匀强磁场的磁感应强度B；
（3）带电质点在磁场中运动的时间．
分析：（2）根据洛仑兹力提供向心力及几何关系即可求解；
（3）粒子在电场中做匀加速，在磁场中做圆周运动，根据匀加速直线运动时间位移公式和圆周运动的周期公式即可解题．
（3）粒子在电场中做匀加速，在磁场中做圆周运动，根据匀加速直线运动时间位移公式和圆周运动的周期公式即可解题．
解答：解：（1）根据左手定则可以知道该磁场的方向垂直纸面向外；
（2）粒子在磁场中完成了如图所示的部分圆运动，设其半径为R，因洛仑兹力提供向心力，
所以有qvB=
由几何关系得
=tan30°
所以r=
=
R
联立以上各式得：B=
（3）设粒子在磁场中运动的时间为t，粒子在磁场中做匀速圆周运动，其周期为T=
=
由于∠MON=120°，所以∠MO'N=60°
故粒子在磁场中运动时间 t=
T=
=
．
答：（1）垂直纸面向外
（2）该匀强磁场的磁感应强度B=
；
（3）带电质点在磁场中运动的时间为t=
（2）粒子在磁场中完成了如图所示的部分圆运动，设其半径为R，因洛仑兹力提供向心力，
所以有qvB=
| mv2 |
| r |
由几何关系得
| R |
| r |
所以r=
| R |
| tan30° |
| 3 |
联立以上各式得：B=
| ||
| 3qR |
（3）设粒子在磁场中运动的时间为t，粒子在磁场中做匀速圆周运动，其周期为T=
| 2πr |
| v |
| 2πm |
| qB |
由于∠MON=120°，所以∠MO'N=60°
故粒子在磁场中运动时间 t=
| 60° |
| 360° |
| πm |
| 3qB |
| ||
| 3V |
答：（1）垂直纸面向外
（2）该匀强磁场的磁感应强度B=
| ||
| 3qR |
（3）带电质点在磁场中运动的时间为t=
| ||
| 3V |
点评：本题主要考查了带电粒子在磁场中运动的问题，要求同学们能正确分析粒子的受力情况，再通过受力情况分析粒子的运动情况，熟练掌握圆周运动及平抛运动的基本公式，难度适中．
练习册系列答案
相关题目
有一匀强磁场分布在以O为中心的一个圆形区域内，磁场方向垂直于xy平面（磁场未画出）．某时刻起一个质量为m、电荷量为+q的带电粒子，由原点O开始运动，初速为v，方向沿x轴正方向．最终粒子到达y轴上的P点，此时速度方向与y轴的夹角为30°，已知OP的距离为L，如图所示．不计重力的影响．
一匀强磁场分布在以O为圆心，半径为R的圆形区域内，方向与纸面垂直，如图所示，质量为m、电荷量q的带正电的质点，经电压为U电场加速后，以一定速度沿半径MO方向进入磁场，沿圆弧运动到N点，然后离开磁场，∠MON=120°，质点所受重力不计，求：
