题目内容
4．关于牛顿第一定律，下列说法中不正确的是（ ）| A． | 牛顿第一定律是实验定律，可以用实验来验证 | |
| B． | 牛顿第一定律表明力是改变物体运动状态的原因 | |
| C． | 惯性定律与惯性是一回事 | |
| D． | 牛顿第一定律是牛顿第二定律的一个特例 |
分析 牛顿第一定律给出了物体不受力作用时的运动规律，同时也说明了力是改变物体运动状态的原因，而不是维持物体运动状态的原因；牛顿第一定律是牛顿在前人实验的基础上，根据逻辑推理得出的，是以实验为基础，但又不是完全通过实验得出．
解答 解：A、牛顿第一定律是牛顿在前人实验的基础上，根据逻辑推理得出的，不能用实验来验证．故A错误；
B、牛顿第一定律告诉我们，一切物体都有保持原来速度不变的性质，力不是维持物体运动的原因，力是改变物体运动状态的原因，故B正确；
C、惯性是由惯性定律（牛顿第一运动定律）所推导出来的物体本身所具有的一种性质，它们的含义并不是完全相同的，故C错误；
D、一切物体在没有受到力的作用时，总保持静止或匀速直线运动状态，这就是牛顿第一定律，不是牛顿第二定律的特例，故D错误．
本题选择不正确的，故选：ACD
点评 牛顿第一运动定律，又称惯性定律，它科学地阐明了力和惯性这两个物理概念，正确地解释了力和运动状态的关系，并提出了一切物体都具有保持其运动状态不变的属性--惯性，它是物理学中一条基本定律．
练习册系列答案
相关题目
3．关于万有引力定律的建立，下列说法中止确的是（ ）
| A． | 牛顿将天体间引力作用的规律推广到自然界中的任何两个物体间 | |
| B． | 引力常量G的大小是牛顿根据大量实验数据得出的 | |
| C． | “月一地检验”表明地面物体所受地球引力与月球所受地球引力遵从同样的规律 | |
| D． | “月一地检验”表明物体在地球上受到地球对它的引力是它在月球上受到月球对它的引力的60倍 |
4．
一竖直放置的轻弹簧，一端固定于地面，一端与质量为3kg的B固定在一起，质量为1kg的物体A放在B上．现在A和B正一起竖直向上运动，如图所示，当A、B分离后，A上升0.2m到达最高点，此时B速度方向向下，弹簧为原长．则从A、B分离起至A到达最高点的这一过程中，弹簧的弹力对B的冲量大小为（g取10m/s2）（ ）
一竖直放置的轻弹簧，一端固定于地面，一端与质量为3kg的B固定在一起，质量为1kg的物体A放在B上．现在A和B正一起竖直向上运动，如图所示，当A、B分离后，A上升0.2m到达最高点，此时B速度方向向下，弹簧为原长．则从A、B分离起至A到达最高点的这一过程中，弹簧的弹力对B的冲量大小为（g取10m/s2）（ ）| A． | 1.2N•s | B． | 8N•s | C． | 6N•s | D． | 4N•s |
1．下列运动速度，属于平均速度的是（ ）
| A． | 刘翔以9.5m/s的速度冲过终点线 | |
| B． | 上海世博会参观高峰时段人流速度约为0.6cm/s | |
| C． | 吴忠市利通区明珠路限速40km/h | |
| D． | 汽车速度计上指示的速度为60km/h |
在水平面内有一小球由M点开始运动，运动方向如图所示，在一水平恒力作用下沿曲线运动到N点，其中vM与vN正好成90°角，在此过程中小球所受的恒力可能是图中的（ ）
16．
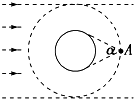宇宙飞船绕地球做圆周运动时，由于地球遮挡阳光，会经历“日全食”过程，如图所示．已知地球的半径为R，地球质量为M，引力常量为G，地球自转周期为T0．太阳光可看作平行光，不考虑地球公转的影响，宇航员在A点测出地球的张角为σ，下列说法中正确的是（ ）
宇宙飞船绕地球做圆周运动时，由于地球遮挡阳光，会经历“日全食”过程，如图所示．已知地球的半径为R，地球质量为M，引力常量为G，地球自转周期为T0．太阳光可看作平行光，不考虑地球公转的影响，宇航员在A点测出地球的张角为σ，下列说法中正确的是（ ）| A． | 飞船的高度为$\frac{R}{sin\frac{σ}{2}}$ | |
| B． | 飞船的线速度为$\sqrt{\frac{GMsin\frac{σ}{2}}{R}}$ | |
| C． | 飞船的周期为2π$\sqrt{\frac{{R}^{3}}{GMsi{n}^{3}\frac{σ}{2}}}$ | |
| D． | 飞船每次“日全食”过程的时间为$\frac{αT0}{2π}$ |
13．
如图所示是一对不等量异种点电荷的电场线分布图，图中两点电荷连线长度为2r，左侧点电荷带电荷量为+2q，右侧点电荷带电荷量为-q，P、Q两点关于两电荷连线对称．由图可知（ ）
如图所示是一对不等量异种点电荷的电场线分布图，图中两点电荷连线长度为2r，左侧点电荷带电荷量为+2q，右侧点电荷带电荷量为-q，P、Q两点关于两电荷连线对称．由图可知（ ）| A． | P、Q两点的电场强度相同 | |
| B． | M点的电场强度大于N点的电场强度 | |
| C． | 把同一试探电荷放在N点，其所受电场力大于放在M点所受的电场力 | |
| D． | 两点电荷连线的中点处的电场强度为2k$\frac{q}{{r}^{2}}$ |
14．
太空中运行的宇宙飞船处于完全失重状态，我国“神舟十号”宇航员王亚平在太空授课时利用质量测量仪完成了测量聂海胜质量的实验．受这一实验启发，某实验小组在实验室也完成了一个不用天平测量物体质量的实验：如图在光滑水平台面右端固定一个永磁恒力器，在台面左端放一辆小车，车上固定一遮光条，遮光条宽度为d，永磁恒力器通过一根细线给小车提供恒定拉力F，使小车由静止开始依次经过两个光电门，光电门1、2记录的挡光时间分别为t1、t2，测得两光电门中心间距为x，不计遮光条质量．根据以上实验数据可得小车质量为（ ）
太空中运行的宇宙飞船处于完全失重状态，我国“神舟十号”宇航员王亚平在太空授课时利用质量测量仪完成了测量聂海胜质量的实验．受这一实验启发，某实验小组在实验室也完成了一个不用天平测量物体质量的实验：如图在光滑水平台面右端固定一个永磁恒力器，在台面左端放一辆小车，车上固定一遮光条，遮光条宽度为d，永磁恒力器通过一根细线给小车提供恒定拉力F，使小车由静止开始依次经过两个光电门，光电门1、2记录的挡光时间分别为t1、t2，测得两光电门中心间距为x，不计遮光条质量．根据以上实验数据可得小车质量为（ ）| A． | $\frac{Fx}{（\frac{d}{{t}_{2}}）^{2}-（\frac{d}{{t}_{1}}）^{2}}$ | B． | $\frac{2Fx}{（\frac{d}{{t}_{2}}）^{2}-（\frac{d}{{t}_{1}}）^{2}}$ | ||
| C． | $\frac{2Fx}{（\frac{d}{{t}_{1}}）^{2}-（\frac{d}{{t}_{2}}）^{2}}$ | D． | $\frac{Fx}{（\frac{d}{{t}_{1}}）^{2}-（\frac{d}{{t}_{2}}）^{2}}$ |