Question

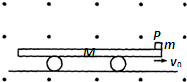（2013?河南模拟）如图所示，足够长的小车质量为M=2kg，置于光滑水平面上．带电荷量为q=-0.4C的可视为质点的物体P 轻放在小车的右端，小车绝缘，物体P 的质量为m=0.2kg．在它们周围空间存在匀强磁场，方向垂直纸面向外，磁感应强度B=0.5T，物体与车之间存在摩擦力，g=10m/s²，今给小车水平向右的瞬时冲量使其获得向右的初速度v₀=16.5m/s，问物体P 能否脱离小车？若不能，求出最后它们一起运动的速度；若能，求脱离后小车的速度．

Answer 1

分析：由于P受摩擦力而被向右加速，运动后受竖直方向的洛伦兹力，当洛伦兹力增大到与重力平衡时，P脱离小车．
假设达到共同速度，根据动量守恒定律求出共同速度进行判断求解．

解答：解：由于P受摩擦力而被向右加速，运动后受竖直方向的洛伦兹力f，
当f增大到与重力平衡时，P脱离小车，设此时P的速度大小是v_P，则：
qv_PB=mg
解得：v_P=10m/s
若达到共同速度，由动量守恒定律得：
Mv₀=（M+m）v_共
解得：v_共=15m/s＞v_P，所以物体P能脱离小车．
P脱离小车时，设小车的速度是v，
根据动量守恒得：
Mv₀=mv_P+Mv
解得：v=15.5m/s
答：物体P能脱离小车，脱离后小车的速度大小是15.5m/s．

点评：解决本题的关键理清物体p的运动情况，知道当洛伦兹力增大到与重力平衡时，P脱离小车，运用动量守恒定律进行求解．