题目内容
如图所示,一辆有四分之一圆弧的小车停在不光滑的水平地面上,质量为m的小球从静止开始由车的顶端无摩擦滑下,且小车始终保持静止状态,地面对小车的静摩擦力最大值是( )
A.

B.

C.mg
D.

【答案】分析:因为小球只有重力做功故小球机械能守恒,由机械能守恒可求得任一位置时的速度,由向心力公式可求得小球受到的支持力;
对小车受力分析可求得静摩擦力的最大值.
解答: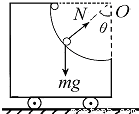 解:设圆弧半径为R,当小球运动到重力与半径夹角为θ时,速度为v.
解:设圆弧半径为R,当小球运动到重力与半径夹角为θ时,速度为v.
根据机械能守恒定律和牛顿第二定律有: mv2=mgRcosθ
mv2=mgRcosθ
N-mgcosθ=m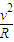
解得小球对小车的压力为:N=3mgcosθ
其水平分量为Nx=3mgcosθsinθ= mgsin2θ
mgsin2θ
根据平衡条件,地面对小车的静摩擦力水平向右,大小为:f=Nx= mgsin2θ
mgsin2θ
可以看出:当sin2θ=1,即θ=45°时,地面对车的静摩擦力最大,其值为fmax= mg;
mg;
故选A.
点评:本题中需要分别对小球和小车进行分析,找出两者间的关系;
本题的难点在于对极值的分析,需要根据题意建立出摩擦力的表达式,再由数学知识求出极值.
对小车受力分析可求得静摩擦力的最大值.
解答:
 解:设圆弧半径为R,当小球运动到重力与半径夹角为θ时,速度为v.
解:设圆弧半径为R,当小球运动到重力与半径夹角为θ时,速度为v.根据机械能守恒定律和牛顿第二定律有:
 mv2=mgRcosθ
mv2=mgRcosθN-mgcosθ=m
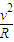
解得小球对小车的压力为:N=3mgcosθ
其水平分量为Nx=3mgcosθsinθ=
 mgsin2θ
mgsin2θ根据平衡条件,地面对小车的静摩擦力水平向右,大小为:f=Nx=
 mgsin2θ
mgsin2θ可以看出:当sin2θ=1,即θ=45°时,地面对车的静摩擦力最大,其值为fmax=
 mg;
mg;故选A.
点评:本题中需要分别对小球和小车进行分析,找出两者间的关系;
本题的难点在于对极值的分析,需要根据题意建立出摩擦力的表达式,再由数学知识求出极值.

练习册系列答案
相关题目

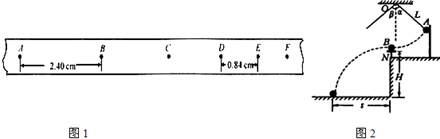 (1)图1是一辆连有纸带的小车做匀变速直线运动时,打点计时器所打的纸带的一部分.打点频率为50Hz,图中A、B、C、D、E、F…是按时间顺序先后确定的计数点(每两个计数点间有四个实验点未画出).用刻度尺量出AB、DE之间的距离分别是2.40cm和0.84cm.
(1)图1是一辆连有纸带的小车做匀变速直线运动时,打点计时器所打的纸带的一部分.打点频率为50Hz,图中A、B、C、D、E、F…是按时间顺序先后确定的计数点(每两个计数点间有四个实验点未画出).用刻度尺量出AB、DE之间的距离分别是2.40cm和0.84cm. 计算出加速度.发现绝大多数情况下,根据公式计算出的加速度要比利用纸带测出的加速度大.若该同学实验操作过程没有错误,试分析其原因.(至少写两点)
计算出加速度.发现绝大多数情况下,根据公式计算出的加速度要比利用纸带测出的加速度大.若该同学实验操作过程没有错误,试分析其原因.(至少写两点)
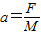 计算出加速度.发现绝大多数情况下,根据公式计算出的加速度要比利用纸带测出的加速度大.若该同学实验操作过程没有错误,试分析其原因.(至少写两点)
计算出加速度.发现绝大多数情况下,根据公式计算出的加速度要比利用纸带测出的加速度大.若该同学实验操作过程没有错误,试分析其原因.(至少写两点)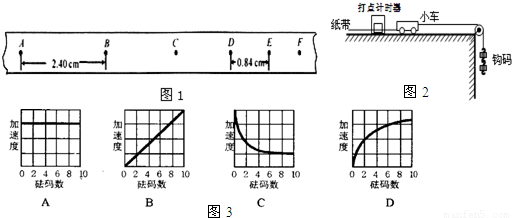



 两点的相对距离不变,相对运动轨迹为圆弧,VA=VB+VAB,在AB连线上
两点的相对距离不变,相对运动轨迹为圆弧,VA=VB+VAB,在AB连线上

