题目内容
如图为翻滚过山车的抽象示意图，大圆环的半径为R，小球从斜轨道的一定高度由静止释放，进入圆轨道后能够完成圆周运动．不及摩擦等阻力．试求h满足什么条件，小球才能顺利完成圆周运动而不脱离轨道？
【答案】分析：要使小球能够通过圆轨道最高点，那么小球在最高点时应该是恰好是物体的重力作为物体的向心力，由向心力的公式可以求得此时的最小的速度，再由机械能守恒可以求得A点离地面的高度h．
解答：解：设在圆轨道最高处的速度为v，则
在圆轨道最高处：mg=m
由机械能守恒定律得：mgh=mg?2R+
mv2?
联立以上各式得h=2.5R
答：h满足h≥2.5R，小球才能顺利完成圆周运动而不脱离轨道．
点评：本题属于圆周运动中绳的模型，在最高点时应该是重力恰好做为圆周运动的向心力，对于圆周运动中的两种模型一定要牢牢的掌握住．
解答：解：设在圆轨道最高处的速度为v，则
在圆轨道最高处：mg=m
由机械能守恒定律得：mgh=mg?2R+
mv2?联立以上各式得h=2.5R
答：h满足h≥2.5R，小球才能顺利完成圆周运动而不脱离轨道．
点评：本题属于圆周运动中绳的模型，在最高点时应该是重力恰好做为圆周运动的向心力，对于圆周运动中的两种模型一定要牢牢的掌握住．
练习册系列答案
初中学业考试导与练系列答案
相关题目
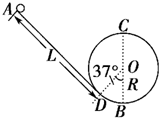“翻滚过山车”的物理原理可以用如图所示装置演示．光滑斜槽轨道AD与半径为R=0.1m的竖直圆轨道（圆心为O）相连，AD与圆O相切于D点，B为轨道的最低点，∠DOB=37°．质量为m=0.1kg的小球从距D点L=1.3m处静止开始下滑，然后冲上光滑的圆形轨道（g=10m/s2，sin37°=0.6，cos37°=0.8）．
如图为翻滚过山车的抽象示意图，大圆环的半径为R，小球从斜轨道的一定高度由静止释放，进入圆轨道后能够完成圆周运动．不计摩擦等阻力．试求h满足什么条件，小球才能顺利完成圆周运动而不脱离轨道？
A．
