题目内容
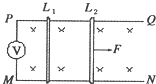如图所示，固定于水平桌面上足够长的两平行光滑导轨PQ、MN，其电阻不计，间距d=0.5m，P、M两端接有一只理想电压表，整个装置处于竖直向下的磁感应强度B0=0.2T的匀强磁场中，两金属棒L1、L2平行地搁在导轨上，其电阻均为r=0.1Ω，质量分别为M1=0.3kg和M2=0.5kg．固定棒L1，使L2在水平恒力F=0.8N的作用下，由静止开始运动．试求：（1）当电压表读数为U=0.2V时，棒L2的加速度为多大；
（2）棒L2能达到的最大速度vm．
分析：（1）由欧姆定律求出电路电流，由安培力公式求出L2受到的安培力，然后由牛顿第二定律求出棒的加速度．
（2）当安培力与拉力平衡时，速度达到最大．
（2）当安培力与拉力平衡时，速度达到最大．
解答：解：（1）L2切割磁感线产生感应电动势，
电压表测L1两端电压，电路电流：
I=
=
=2A，
L2所受的安培力：
FB=BId=0.2×2×0.5=0.2N，
对L2由牛顿第二定律得：F-FB=m2a，
解得，L2的加速度：a=
=
=1.2m/s2；
（2）当杆做匀速直线运动时，棒L2速度达到最大，此时电路电流为Im，
L2切割磁感线产生感应电动势：E=Bdvm，
电路电流Im=
，
安培力：FB=BImd=
，
杆做匀速直线运动，由平衡条件得：
F=FB，即：F=
，
解得：vm=
=16m/s；
答：（1）当电压表读数为U=0.2V时，棒L2的加速度为1.2m/s2；（2）棒L2能达到的最大速度为16m/s．
电压表测L1两端电压，电路电流：
I=
| U |
| r |
| 0.2V |
| 0.1Ω |
L2所受的安培力：
FB=BId=0.2×2×0.5=0.2N，
对L2由牛顿第二定律得：F-FB=m2a，
解得，L2的加速度：a=
| F-FB |
| m2 |
| 0.8-0.2 |
| 0.5 |
（2）当杆做匀速直线运动时，棒L2速度达到最大，此时电路电流为Im，
L2切割磁感线产生感应电动势：E=Bdvm，
电路电流Im=
| Bdvm |
| 2r |
安培力：FB=BImd=
| B2d2vm |
| 2r |
杆做匀速直线运动，由平衡条件得：
F=FB，即：F=
| B2d2vm |
| 2r |
解得：vm=
| 2Fr |
| B2d2 |
答：（1）当电压表读数为U=0.2V时，棒L2的加速度为1.2m/s2；（2）棒L2能达到的最大速度为16m/s．
点评：本题考查了求导体棒的加速度、导体棒的最大速度，分析清楚金属杆的运动过程是正确解题的前提与关键；当金属杆受到的安培力与拉力相等时，杆做匀速直线运动，速度达到最大．
练习册系列答案
相关题目
如图所示，固定于水平桌面上的金属框架cdef，处在竖直向下的匀强磁场中，金属棒ab搁在框架上，可无摩擦滑动．此时abed构成一个边长为L的正方形，棒的电阻为r，其余部分电阻不计．开始时磁感应强度为B0．
（2010?盐城三模）如图所示，固定于水平面的U型金属导轨abcd，电阻不计，导轨间距L=1.0m，左端接有电阻R=2Ω．金属杆PQ的质量m=0.2Kg，电阻r=1Ω，与导轨间动摩擦因数μ=0.2，滑动时保持与导轨垂直．在水平面上建立x0y坐标系，x≥0的空间存在竖直向下的磁场，磁感应强度仅随横坐标x变化．金属杆受水平恒力F=2.4N的作用，从坐标原点开始以初速度v0=1.0m/s向右作匀加速运动，经t1=0.4s到达x1=0.8m处，g取10m/s2．
如图所示，固定于水平桌面上足够长的两平行导轨PO、MN，PQ、MN的电阻不计，间距为d=0.5m．P、M两端接有一只理想电压表，整个装置处于竖直向下的磁感应强度B=0.2T的匀强磁场中．电阻均为r=0.1Ω，质量分别为m1=300g和m2=500g的两金属棒L1、L2平行的搁在光滑导轨上，现固定棒L1，L2在水平恒力F=0.8N的作用下，由静止开始做加速运动，试求：
（2010?宿州二模）如图所示，固定于水平面上的金属架CDEF处在竖直向下的匀强磁场中，金属棒MN沿框架以某一速度向右做匀速运动．t=0时，磁感应强度为B0，此时MN到达的位置恰好使MDEN构成一个边长为L的正方形．为使MN棒中不产生感应电流，从t=0开始，磁感应强度B随时间t的变化的图象正确的是（ ）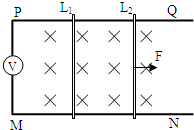
如图所示，固定于水平桌面上足够长的两平行导轨PQ、MN，PQ、MN的电阻不计，间距为d=0.5m，PM两端接有一理想电压表，整个装置处于竖直向下的匀强磁场中，磁感应强度为B=0.2T，电阻均为R=0.1Ω、质量分别为m1=300g 和m2=500g的两金属棒L1、L2平行地搁在光滑的导轨上，现固定L1，L2在水平恒力F=0.8N的作用下，由静止开始作加速运动．试求：