题目内容
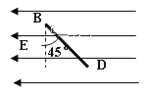
【题目】一宇航员站在某质量分布均匀的星球表面的斜坡上的 P 点沿水平方向以初速度 
抛出一个小球，测得小球经时间 t 落到斜坡上另一点 Q，斜面的倾角为 α，已知该星球半径为 R，万有引力常量为 G，求：
（1）该星球表面的重力加速度为___________；
（2）该星球的密度______________；
（3）该星球的第一宇宙速度______________；
（4）人造卫星绕该星球表面做匀速圆周运动的最小周期_______________。
【答案】
【解析】
解：(1)设该星球表现的重力加速度为
，根据平抛运动规律：
水平方向：
竖直方向：
平抛位移与水平方向的夹角的正切值：
解得：
(2)在星球表面有：
解得：
该星球的密度：
(3) 根据万有应力提供向心力，万有应力等于重力，则有：
可得：
该星球的第一宇宙速度：
(4)绕星球表面运行的卫星具有最小的周期，即：
练习册系列答案
名题金卷系列答案
相关题目
