题目内容
13.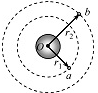 如图所示,若两颗人造卫星a和b均绕地球做匀速圆周运动,a、b到地心O的距离分别为r1、r2,线速度大小分别为v1、v2,角速度大小分别为ω1、ω2,向心加速度大小分别为a1、a2,周期大小分别为T1、T2,下列说法正确的是( )
如图所示,若两颗人造卫星a和b均绕地球做匀速圆周运动,a、b到地心O的距离分别为r1、r2,线速度大小分别为v1、v2,角速度大小分别为ω1、ω2,向心加速度大小分别为a1、a2,周期大小分别为T1、T2,下列说法正确的是( )| A. | $\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{{r}_{1}}{{r}_{2}}}$ | B. | $\frac{{ω}_{1}}{{ω}_{2}}$=$\sqrt{(\frac{{r}_{2}}{{r}_{1}})^{3}}$ | C. | $\frac{{a}_{1}}{{a}_{2}}$=($\frac{{r}_{2}}{{r}_{1}}$)3 | D. | $\frac{{T}_{1}}{{T}_{2}}$=$\sqrt{(\frac{{r}_{1}}{{r}_{2}})}$3 |
分析 人造卫星a和b均绕地球做匀速圆周运动,根据万有引力提供向心力,列式解出线速度、角速度、向心加速度、周期与轨道半径r的关系式,再进行求解.
解答 解:根据万有引力提供向心力得:G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$=mω2r=ma=m$\frac{4{π}^{2}}{{T}^{2}}$r
解得:v=$\sqrt{\frac{GM}{r}}$,ω=$\sqrt{\frac{GM}{{r}^{3}}}$,a=$\frac{GM}{{r}^{2}}$,T=2π$\sqrt{\frac{{r}^{3}}{GM}}$
据题,a、b到地心O的距离分别为r1、r2,可得:$\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{{r}_{2}}{{r}_{1}}}$,$\frac{{ω}_{1}}{{ω}_{2}}$=$\sqrt{(\frac{{r}_{2}}{{r}_{1}})^{3}}$,$\frac{{a}_{1}}{{a}_{2}}$=$(\frac{{r}_{2}}{{r}_{1}})^{2}$,$\frac{{T}_{1}}{{T}_{2}}$=$\sqrt{(\frac{{r}_{1}}{{r}_{2}})}$3
故选:BD
点评 本题关键是要掌握万有引力提供向心力这个关系,能够根据题意选择恰当的向心力的表达式.

练习册系列答案
相关题目
20.观察某洗衣机的铭牌,解答下列问题:
(1)该洗衣机适用于直流电源还是交流电源?正常工作电压多大?
(2)正常洗涤时,通过洗衣机的电流多大?
(3)给水加热的电阻丝电阻有多大?
| 防触电保护类别Ⅰ类 | 额定洗涤容量5 kg | |
| 额定电压220 V | 电源频率50 Hz | |
| 洗涤功率330 W | 甩干功率650 W | |
| 水加热功率2420 W | 最大工作电流10 A | |
| 自来水压力 0.05 MPa≤p≤1 MPa | 重量72 kg | |
| 出厂日期:2013年8月28日 | ||
| 出厂编号:970828253 | ||
(2)正常洗涤时,通过洗衣机的电流多大?
(3)给水加热的电阻丝电阻有多大?
1.两个紧密接触的粗糙物体,发生相对滑动时,两者间的一对滑动摩擦力做功之和( )
| A. | 一定为负 | B. | 一定为零 | C. | 可能为正 | D. | 可能为零 |
1. 图示为气流加热装置的示意图,使用电阻丝加热导气管,变压器可视为理想变压器,原线圈接入电压有效值恒定的交流电,调节触头P,使输出功率由1000W降至250W.则调节前后( )
图示为气流加热装置的示意图,使用电阻丝加热导气管,变压器可视为理想变压器,原线圈接入电压有效值恒定的交流电,调节触头P,使输出功率由1000W降至250W.则调节前后( )
 图示为气流加热装置的示意图,使用电阻丝加热导气管,变压器可视为理想变压器,原线圈接入电压有效值恒定的交流电,调节触头P,使输出功率由1000W降至250W.则调节前后( )
图示为气流加热装置的示意图,使用电阻丝加热导气管,变压器可视为理想变压器,原线圈接入电压有效值恒定的交流电,调节触头P,使输出功率由1000W降至250W.则调节前后( )| A. | 副线圈两端的电压比为4:1 | B. | 原线圈输入电流比为1:2 | ||
| C. | 副线圈的接入匝数比为2:1 | D. | 原线圈输入功率比为2:1 |
8.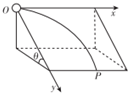 质点以v0由坐标原点O沿Ox方向抛出,沿光滑斜面运动,落地点为P,不计阻力,如图所示.改变光滑斜面的倾角,使θ分别为30°、45°、60°,但斜面高度始终不变,水平初速度v0不变.在这三种情景下落地时质点运动的水平位移分别为x1、x2、x3,质点运动的时间t1、t2、t3.下列判断正确的是( )
质点以v0由坐标原点O沿Ox方向抛出,沿光滑斜面运动,落地点为P,不计阻力,如图所示.改变光滑斜面的倾角,使θ分别为30°、45°、60°,但斜面高度始终不变,水平初速度v0不变.在这三种情景下落地时质点运动的水平位移分别为x1、x2、x3,质点运动的时间t1、t2、t3.下列判断正确的是( )
 质点以v0由坐标原点O沿Ox方向抛出,沿光滑斜面运动,落地点为P,不计阻力,如图所示.改变光滑斜面的倾角,使θ分别为30°、45°、60°,但斜面高度始终不变,水平初速度v0不变.在这三种情景下落地时质点运动的水平位移分别为x1、x2、x3,质点运动的时间t1、t2、t3.下列判断正确的是( )
质点以v0由坐标原点O沿Ox方向抛出,沿光滑斜面运动,落地点为P,不计阻力,如图所示.改变光滑斜面的倾角,使θ分别为30°、45°、60°,但斜面高度始终不变,水平初速度v0不变.在这三种情景下落地时质点运动的水平位移分别为x1、x2、x3,质点运动的时间t1、t2、t3.下列判断正确的是( )| A. | t1>t2>t3 | B. | x1>x2>x3 | ||
| C. | 落地时质点的速度与x轴夹角相同 | D. | 落地时质点重力的功率相同 |
18. “天宫一号”目标飞行器与“神舟十号”飞船自动交会对接的示意图如图所示,圆形轨道Ⅰ为“天宫一号”运行轨道,圆形轨道Ⅱ为“神舟十号”运行轨道,在实现交会对接前,“神舟十号”要进行多次变轨,则( )
“天宫一号”目标飞行器与“神舟十号”飞船自动交会对接的示意图如图所示,圆形轨道Ⅰ为“天宫一号”运行轨道,圆形轨道Ⅱ为“神舟十号”运行轨道,在实现交会对接前,“神舟十号”要进行多次变轨,则( )
 “天宫一号”目标飞行器与“神舟十号”飞船自动交会对接的示意图如图所示,圆形轨道Ⅰ为“天宫一号”运行轨道,圆形轨道Ⅱ为“神舟十号”运行轨道,在实现交会对接前,“神舟十号”要进行多次变轨,则( )
“天宫一号”目标飞行器与“神舟十号”飞船自动交会对接的示意图如图所示,圆形轨道Ⅰ为“天宫一号”运行轨道,圆形轨道Ⅱ为“神舟十号”运行轨道,在实现交会对接前,“神舟十号”要进行多次变轨,则( )| A. | “天宫一号”的运行速率大于“神舟十号”在轨道Ⅱ上的运行速率 | |
| B. | “神舟十号”变轨前后的机械能守恒 | |
| C. | “神舟十号”可以通过减速而使轨道半径变大 | |
| D. | “天宫一号”和“神舟十号”对接瞬间的向心加速度相同 |
5.以下说法正确的是( )
| A. | 电荷处于磁场中不一定受到洛伦兹力 | |
| B. | 电荷在磁场中一定受到洛伦兹力 | |
| C. | 某运动电荷在某处未受到洛伦兹力,该处的磁感成强度一定为零 | |
| D. | 洛伦兹力不能改变运动电荷的速度 |
2. 北京时间2012年10月15日凌晨,奥地利极限运动员费力克斯乘气球升至约3.9万米的高空后,带着降落伞跳下并成功落地,如图为他纵身跳下的一瞬间.若降落伞打开前费力克斯做加速运动,降落伞打开后费力克斯做减速运动,下列说法正确的是( )
北京时间2012年10月15日凌晨,奥地利极限运动员费力克斯乘气球升至约3.9万米的高空后,带着降落伞跳下并成功落地,如图为他纵身跳下的一瞬间.若降落伞打开前费力克斯做加速运动,降落伞打开后费力克斯做减速运动,下列说法正确的是( )
 北京时间2012年10月15日凌晨,奥地利极限运动员费力克斯乘气球升至约3.9万米的高空后,带着降落伞跳下并成功落地,如图为他纵身跳下的一瞬间.若降落伞打开前费力克斯做加速运动,降落伞打开后费力克斯做减速运动,下列说法正确的是( )
北京时间2012年10月15日凌晨,奥地利极限运动员费力克斯乘气球升至约3.9万米的高空后,带着降落伞跳下并成功落地,如图为他纵身跳下的一瞬间.若降落伞打开前费力克斯做加速运动,降落伞打开后费力克斯做减速运动,下列说法正确的是( )| A. | 在降落伞打开前,菲力克斯处于超重状态 | |
| B. | 在降落伞打开前,菲力克斯处于失重状态 | |
| C. | 在降落伞打开后,菲力克斯受到的阻力等于他的重力 | |
| D. | 在降落伞打开后,菲力克斯受到的阻力小于他的重力 |
3. 如图所示,一平行板电容器,右极板接电源正极,板长为2d,板间距离为d.一带电量为q、质量为m的负离子(重力不计)以速度v0贴近左极板沿极板方向射入,恰从右极板下边缘射出.在右极板右侧空间存在垂直纸面方向的匀强磁场(未标出).要使该负离子在磁场中运动后,又恰能直接从右极板上边缘进入电场,则( )
如图所示,一平行板电容器,右极板接电源正极,板长为2d,板间距离为d.一带电量为q、质量为m的负离子(重力不计)以速度v0贴近左极板沿极板方向射入,恰从右极板下边缘射出.在右极板右侧空间存在垂直纸面方向的匀强磁场(未标出).要使该负离子在磁场中运动后,又恰能直接从右极板上边缘进入电场,则( )
 如图所示,一平行板电容器,右极板接电源正极,板长为2d,板间距离为d.一带电量为q、质量为m的负离子(重力不计)以速度v0贴近左极板沿极板方向射入,恰从右极板下边缘射出.在右极板右侧空间存在垂直纸面方向的匀强磁场(未标出).要使该负离子在磁场中运动后,又恰能直接从右极板上边缘进入电场,则( )
如图所示,一平行板电容器,右极板接电源正极,板长为2d,板间距离为d.一带电量为q、质量为m的负离子(重力不计)以速度v0贴近左极板沿极板方向射入,恰从右极板下边缘射出.在右极板右侧空间存在垂直纸面方向的匀强磁场(未标出).要使该负离子在磁场中运动后,又恰能直接从右极板上边缘进入电场,则( )| A. | 磁场方向垂直纸面向里 | |
| B. | 磁场方向垂直纸面向外,向里都有可能 | |
| C. | 磁感应强度大小为$\frac{{m{v_0}}}{qd}$ | |
| D. | 在磁场中运动时间为$\frac{{3\sqrt{2}πd}}{{2{v_0}}}$ |