题目内容
8.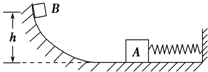 如图所示,轻质弹簧的一端固定在墙上,另一端与质量为m的物体A相连,A放在光滑水平面上,有一质量与A相同的物体B,从高h处由静止开始沿光滑曲面滑下,与A相碰后一起将弹簧压缩,弹簧复原过程中某时刻B与A分开且沿原曲面上升.下列正确的是( )
如图所示,轻质弹簧的一端固定在墙上,另一端与质量为m的物体A相连,A放在光滑水平面上,有一质量与A相同的物体B,从高h处由静止开始沿光滑曲面滑下,与A相碰后一起将弹簧压缩,弹簧复原过程中某时刻B与A分开且沿原曲面上升.下列正确的是( )| A. | 弹簧被压缩时所具有的最大弹性势能为mgh | |
| B. | 弹簧被压缩时所具有的最大弹性势能为$\frac{mgh}{2}$ | |
| C. | B能达到的最大高度为$\frac{h}{2}$ | |
| D. | B能达到的最大高度为$\frac{h}{4}$ |
分析 B从轨道上下滑过程,只有重力做功,机械能守恒.运用机械能守恒定律可求得B与A碰撞前的速度.两个物体碰撞过程动量守恒,即可求得碰后的共同速度.碰后共同体压缩弹簧,当速度为零,弹簧的压缩量最大,弹性势能最大,根据系统的机械能守恒求得最大的弹性势能.当弹簧再次恢复原长时,A与B将分开,根据机械能守恒求得B能达到的最大高度.
解答 解:AB、对B下滑过程,据机械能守恒定律可得:mgh=$\frac{1}{2}m{v}_{0}^{2}$,则得,B刚到达水平地面时的速度 v0=$\sqrt{2gh}$.
A碰撞过程,以A、B组成的系统为研究对象,取向右为正方向,根据动量守恒定律可得:
mv0=2mv,得A与B碰撞后的共同速度为 v=$\frac{1}{2}$v0,所以弹簧被压缩时所具有的最大弹性势能为 Epm=$\frac{1}{2}$•2mv2=$\frac{mgh}{2}$,故A错误,B正确;
CD、当弹簧再次恢复原长时,A与B将分开,B以v的速度沿斜面上滑,根据机械能守恒定律可得 mgh′=$\frac{1}{2}$mv2,解得,B能达到的最大高度为 h′=$\frac{h}{4}$,故C错误,D正确.
故选:BD
点评 利用动量守恒定律解题,一定注意状态的变化和状态的分析,明确研究对象,并选取正方向.把动量守恒和机械能守恒结合起来列出等式求解是常见的问题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
19. 如图所示,重20N的物体放在粗糙水平面上,用F=8N的力斜向下推物体.F与水平面成30°角,物体与水平面间的动摩擦因数μ=0.5,则( )
如图所示,重20N的物体放在粗糙水平面上,用F=8N的力斜向下推物体.F与水平面成30°角,物体与水平面间的动摩擦因数μ=0.5,则( )
 如图所示,重20N的物体放在粗糙水平面上,用F=8N的力斜向下推物体.F与水平面成30°角,物体与水平面间的动摩擦因数μ=0.5,则( )
如图所示,重20N的物体放在粗糙水平面上,用F=8N的力斜向下推物体.F与水平面成30°角,物体与水平面间的动摩擦因数μ=0.5,则( )| A. | 物体对地面的压力为20N | B. | 物体所受的摩擦力为12N | ||
| C. | 物体所受的合力为零 | D. | 以上说法都不对 |
3.关于重力做功和物体的重力势能,下列说法不正确的是( )
| A. | 当重力对物体做正功时,物体的重力势能一定减少 | |
| B. | 物体克服重力做功时,物体的重力势能一定增加 | |
| C. | 地球上的物体的重力势能都只有一个唯一确定的值 | |
| D. | 重力做功的多少与参考平面的选取无关 |
13. 图为一注水的玻璃装置,玻璃管D、E上端与大气相通,利用玻璃管C使A、B两球上部相通,D、C、E三管与两球接口处紧密封接.当A、B、D的水面高度差如图所示时,E管内水面相对B中水面的高度差h应等于( )
图为一注水的玻璃装置,玻璃管D、E上端与大气相通,利用玻璃管C使A、B两球上部相通,D、C、E三管与两球接口处紧密封接.当A、B、D的水面高度差如图所示时,E管内水面相对B中水面的高度差h应等于( )
 图为一注水的玻璃装置,玻璃管D、E上端与大气相通,利用玻璃管C使A、B两球上部相通,D、C、E三管与两球接口处紧密封接.当A、B、D的水面高度差如图所示时,E管内水面相对B中水面的高度差h应等于( )
图为一注水的玻璃装置,玻璃管D、E上端与大气相通,利用玻璃管C使A、B两球上部相通,D、C、E三管与两球接口处紧密封接.当A、B、D的水面高度差如图所示时,E管内水面相对B中水面的高度差h应等于( )| A. | 2m | B. | 0.5m | C. | 1m | D. | 1.5m |
20.如果将两个分子看成质点,当这两个分子之间的距离为r0时分子力为零,则分子力F及分子势能EP随着分子间距离r的变化而变化的情况是( )
| A. | 当r<r0时,随着r变小,F变大,EP变小 | |
| B. | 当r<r0时,随着r变小,F变大,EP变大 | |
| C. | 当r>r0时,随着r变大,F变大,EP变大 | |
| D. | 当r>r0时,随着r变大,F变小,EP变小 |
18.下列说法中正确的是( )
| A. | 在光发生折射现象时,折射角不一定小于入射角 | |
| B. | 某介质的折射率与入射角的正弦值成正比,与折射角的正弦值成反比 | |
| C. | 在光发生折射现象时,入射角增大到原来的2倍,折射角也增大到原来的2倍 | |
| D. | 当光以60°的入射角从介质a到另一种介质b时,折射角为45°;那么当光以45°的入射角从介质a到另介质b时,折射角为30° |
 电流表和电压表都是由小量程的电流表(表头)改装成的.如图所示,有一表头,满偏电流Ig=500 μA,内阻Rg=200Ω,.用它作多用电表的表头,已知R1=20Ω,R2=180Ω,R3=49.9kΩ,R4=499.9kΩ.
电流表和电压表都是由小量程的电流表(表头)改装成的.如图所示,有一表头,满偏电流Ig=500 μA,内阻Rg=200Ω,.用它作多用电表的表头,已知R1=20Ω,R2=180Ω,R3=49.9kΩ,R4=499.9kΩ. 游乐场中有一类似于过山车的设施.简易模型如图所示,它由倾角为α=37°的光滑斜面轨道、水平轨道和竖直平面内的光滑圆形轨道组成,A、B分别是斜面与圆形轨道的最低点(且A处有一极小光滑圆弧与轨道相切),A、B两点相距L=4.25m.一个质量为m=0.1kg的小球(视为质点),从斜面上距A点h=4.05m高处由静止下滑,小球与水平轨道的动摩擦因数μ=0.2.假设水平轨道足够长,不考虑斜面轨道与圆形轨道相互重叠时对小球运动的影响,sin37°=0.6,g取lOm/s2.求:
游乐场中有一类似于过山车的设施.简易模型如图所示,它由倾角为α=37°的光滑斜面轨道、水平轨道和竖直平面内的光滑圆形轨道组成,A、B分别是斜面与圆形轨道的最低点(且A处有一极小光滑圆弧与轨道相切),A、B两点相距L=4.25m.一个质量为m=0.1kg的小球(视为质点),从斜面上距A点h=4.05m高处由静止下滑,小球与水平轨道的动摩擦因数μ=0.2.假设水平轨道足够长,不考虑斜面轨道与圆形轨道相互重叠时对小球运动的影响,sin37°=0.6,g取lOm/s2.求: