题目内容
在离地面H=10m高的平台边缘，以v0=12m/s的速度竖直向上抛出一个小球，小球上升到最高点时比平台高出h=6m，若空气阻力f大小不变，g=10m/s2．求：
（1）空气阻力与小球重力大小的比值
．
（2）小球从抛出到落到地面所经过的时间t．
（1）空气阻力与小球重力大小的比值
| f | mg |
（2）小球从抛出到落到地面所经过的时间t．
分析：（1）在上升过程中由运动学公式可求出上升的加速度，再由牛顿第二定律求出空气阻力，即可求出比值；
（2）在从最高点下落过程中，由牛顿第二定律求出下落加速度，再由运动学公式求出下落时间；
（2）在从最高点下落过程中，由牛顿第二定律求出下落加速度，再由运动学公式求出下落时间；
解答：解：（1）从抛出到最高点，2a1h=v02
代入数据求得a1=
=
m/s2=12m/s2
根据牛顿第二定律：mg+f=ma1
f=ma1-mg=m（12-10）=2m
=
=0.2
（2）上升过程所用时间t1=
=
s=1s
下落过程加速度a2=
=
=8m/s2
下落过程所用时间t2 h+H=
a2
得t2=
=
s=2s
总时间 t=t1+t2=3s
答：（1）空气阻力与小球重力大小的比值为0.2．
（2）小球从抛出到落到地面所经过的时间t为3s．
代入数据求得a1=
| v20 |
| 2h |
| 122 |
| 2×6 |
根据牛顿第二定律：mg+f=ma1
f=ma1-mg=m（12-10）=2m
| f |
| mg |
| 2m |
| 10m |
（2）上升过程所用时间t1=
| v0 |
| a1 |
| 12 |
| 12 |
下落过程加速度a2=
| mg-f |
| m |
| 10m-2m |
| m |
下落过程所用时间t2 h+H=
| 1 |
| 2 |
| t | 2 2 |
得t2=
|
|
总时间 t=t1+t2=3s
答：（1）空气阻力与小球重力大小的比值为0.2．
（2）小球从抛出到落到地面所经过的时间t为3s．
点评：本题主要考查两个运动过程，上升过程和下降过程，分别利用牛顿第二定律和运动学公式即可求的．
练习册系列答案
名校课堂系列答案
相关题目
某滑板爱好者在离地面h=1.8m高的平台上滑行，以某一水平初速度离开A点后落在水平地面上的B点，其水平位移S1=3m．着地时由于存在能量损失，着地后速度变为v=4m/s，并以此为初速度沿水平面滑行S2=8m后停止．已知人与滑板的总质量m=70kg，空气阻力忽略不计，取g=10m/s2．求：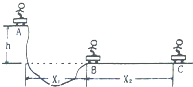
如图所示，某滑板爱好者在离地面h=3.2m高的平台上滑行，水平离开A点后落在水平面上的B点，其水平位移X1=4m，着地时由于存在机械能损失，着地后速度大小变为v=4m/s，并以此为初速度沿水平地面滑行X2=4m后停止运动．已知人与滑板的总质量m=50kg（不计空气阻力，g取10m/s2）．求：（1）人与滑板离开平台时的水平初速度大小；
面上的B点，其水平位移S1 = 3m。着地时由于存在能量损失，着地后速度变为v= 4m/s，并以此为初速度沿水平面滑行S2 = 8m后停止。已知人与滑板的总质量m = 70kg，空气阻力忽略不计，取g = 10m/s2。求：