题目内容
(1)一列横波沿直线传播,在波的传播方向上有A、B两点.在t时刻A、B两点间形成的波形如图甲所示,在(t+3s)时刻A、B两点间形成的波形如图乙所示,已知A、B两点间距离S=9m,则以下说法中正确的是______
A.若周期为4s,波一定向右传播
B.若周期大于4s,波可能向右传播
C.若波速为8.5m/s,波一定向左传播
D.该波波速可能的最小值为0.5m/s
(2)如图所示,直角玻璃三棱镜置于空气中,已知∠A=60°,∠C=90°;一束极细的光于AC边的中点垂直AC面入射,
 ,棱镜的折射率为n=
,棱镜的折射率为n= ,求光第一次从BC面射出时:
,求光第一次从BC面射出时:①光的折射角.
②光在棱镜中传播的时间(设光在真空中传播速度为c)

【答案】分析:(1)根据两时刻的波形,列出周期通项,得到波速的通项,再分析特殊值确定波的传播方向.
(2)①根据折射率求出临界角C=45°,光射到AB面时入射角大于临界角C,发生全反射,从BC面射出,作出光路图,确定入射角,由折射率求出光的折射角.②根据几何知识求出光在棱镜中传播的距离,由折射率光在棱镜中的速度,再求时间.
解答:解:(1)A、若波向右传播,3s=(n+ )T1,(n=0,1,2,、、、),T1=
)T1,(n=0,1,2,、、、),T1=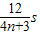
若波向左传播,3s=(n+ )T2,(n=0,1,2,、、、),T2=
)T2,(n=0,1,2,、、、),T2=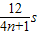
由于n是整数,当T=3s时,符合T1通项,波向右传播.故A正确.
B、由上分析,波向右传播周期T≤4s.故B错误.
C、由图波长λ=6m,若波速为8.5m/s,波传播的距离为x=vt=8.5×3m=25.5m=4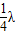 ,根据波形的平移,波一定向左传播.故C正确.
,根据波形的平移,波一定向左传播.故C正确.
D、波传播的最大距离为向左传播1.5m,波波速可能的最小值为v=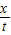 =
=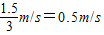 .故D正确.
.故D正确.
故选ACD
(2)①设棱镜的临界角为C
则sinC=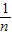 =
=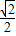 ,C=45°则光线射到AB面时发生全反射.作出光路图,由反射定律和几何知识得∠4=30°,
,C=45°则光线射到AB面时发生全反射.作出光路图,由反射定律和几何知识得∠4=30°,
则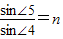 ,代入解得∠5=45°
,代入解得∠5=45°
故光第一次从BC面射出时光的折射角为45°.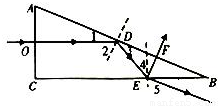
②由数学知识,OD=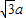 ,DE=
,DE=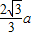
光在棱镜中的速度v=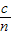
光在棱镜中传播的时间为t=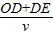 =
=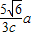
答:(1)ACD
(2)①光的折射角为45°.
②光在棱镜中传播的时间为=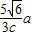 .
.
点评:当光从介质射向真空时,要考虑能否发生全反射.几何光学作出光路图是解题的关键.
(2)①根据折射率求出临界角C=45°,光射到AB面时入射角大于临界角C,发生全反射,从BC面射出,作出光路图,确定入射角,由折射率求出光的折射角.②根据几何知识求出光在棱镜中传播的距离,由折射率光在棱镜中的速度,再求时间.
解答:解:(1)A、若波向右传播,3s=(n+
 )T1,(n=0,1,2,、、、),T1=
)T1,(n=0,1,2,、、、),T1=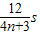
若波向左传播,3s=(n+
 )T2,(n=0,1,2,、、、),T2=
)T2,(n=0,1,2,、、、),T2=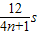
由于n是整数,当T=3s时,符合T1通项,波向右传播.故A正确.
B、由上分析,波向右传播周期T≤4s.故B错误.
C、由图波长λ=6m,若波速为8.5m/s,波传播的距离为x=vt=8.5×3m=25.5m=4
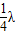 ,根据波形的平移,波一定向左传播.故C正确.
,根据波形的平移,波一定向左传播.故C正确.D、波传播的最大距离为向左传播1.5m,波波速可能的最小值为v=
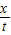 =
=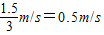 .故D正确.
.故D正确.故选ACD
(2)①设棱镜的临界角为C
则sinC=
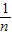 =
=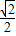 ,C=45°则光线射到AB面时发生全反射.作出光路图,由反射定律和几何知识得∠4=30°,
,C=45°则光线射到AB面时发生全反射.作出光路图,由反射定律和几何知识得∠4=30°,则
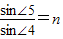 ,代入解得∠5=45°
,代入解得∠5=45°故光第一次从BC面射出时光的折射角为45°.

②由数学知识,OD=
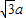 ,DE=
,DE=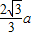
光在棱镜中的速度v=
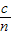
光在棱镜中传播的时间为t=
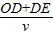 =
=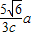
答:(1)ACD
(2)①光的折射角为45°.
②光在棱镜中传播的时间为=
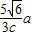 .
.点评:当光从介质射向真空时,要考虑能否发生全反射.几何光学作出光路图是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012?许昌模拟)(1)一列横波沿直线传播,在波的传播方向上有A、B两点.在t时刻A、B两点间形成的波形如图甲所示,在
(2012?许昌模拟)(1)一列横波沿直线传播,在波的传播方向上有A、B两点.在t时刻A、B两点间形成的波形如图甲所示,在

 ,棱镜的折射率为n=
,棱镜的折射率为n= ,求光第一次从BC面射出时:
,求光第一次从BC面射出时: