Question

如下图所示，处于平直轨道上的甲、乙两物体相距s，同时同向开始运动，甲以初速度v₁，加速度a₁作匀加速运动，乙以初速度为零，加速度为a₂做匀加速运动，下述情况可能发生的是(假定甲能从乙旁边通过互不影响)

[　　]

A．a₁＝a₂能相遇一次　　  B．a₁＞a₂能相遇两次

C．a₁＜a₂可能相遇一次    D．a₁＜a₂可能相遇二次

Answer 1

答案：ACD
解析：

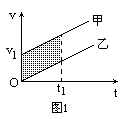
解析　本题属相遇问题，求解方法可以用公式(代数法)，分别列出甲、乙的位移方程及相遇时的位移关系方程，再联立求解、讨论．也可以用图像法(几何法)，结合v－t图像分析，这种方法很直观，尤其是本题只需进行定性判断，用图像法能迅速求解． 　　解法一：公式法 　　设经时间t，甲、乙相遇，时间t内甲、乙位移分别为： 　　s1＝v1t＋a1t2　　　　　　　　(1) 　　s2＝a2t2　　　　　　　　　　(2) 　　相遇时位移满足s1＝s2＋s　　　(3) 　　由(1)(2)(3)解得 　　(a1－a2)t2＋2v1t－2s＝0　　　　(4) 　　讨论：①当a1＝a2时，(4)变为一元一次方程，t有一解t＝，即表示甲、乙只相遇一次． 　　②当a1≠a2时，(4)为关于时间t的一元二次方程，由求根公式得 　　t＝ 　　当a1＞a2时，t的两个根中一正一负，合理解为t＞0，故只有一个解，即只能相遇一次． 　　当a1＜a2时， 　　t＝， 　　这时解的情况比较复杂．若Δ＝4－8(a2－a1)s＜0，方程无解，即表示不可能相遇．若Δ＝0，t有惟一解且t＞0，表示相遇一次；若Δ＞0，方程有两解，可能两根一正一负，取合理解t＞0，故只能相遇一次；也可能两根均为正，表示相遇两次． 　　根据以上分析，本题选A、C、D 　　解法二：图像法 　　我们画出满足题给条件的v－t图像． 　　图1对应a1＝a2的情况，两条图线平行，两物体仅在t＝t1时相遇一次．图中阴影部分面积为S． 　　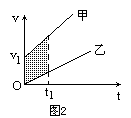图2对应a1＞a2的情况，两物体仅在t＝t2时相遇一次． 　　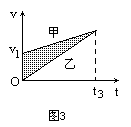在图3对应a1＜a2的情况，若在两条图线的交点对应的时刻t3两物体相遇，则仅相遇一次．图中阴影部分面积为S．若图中阴影面积小于S，由甲、乙不可能相遇．若图中阴影部分面积大于S，则可能相遇两次． 　　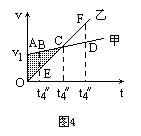如图4，在t4和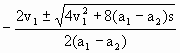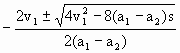两个时刻均相遇．图中四边形ABEO的面积等于S，在0－t4时间内，甲在后，乙在前，v甲＞v乙，甲追赶乙，距离逐渐减小，在t4时刻，甲、乙相遇．在t4－时间内，甲在前，乙在后．甲将乙拉得越来越远．－时间内，甲在前，乙在后，v乙＞v甲，乙追甲，距离逐渐减小，到时刻甲、乙再次相遇．当t＞后，乙在前，甲在后，v乙＞v甲，两者距离一直变大，不可能再相遇．图中S△BCE为从第一次相遇后，甲把乙拉开的距离，S△FCD为从起乙追上甲的距离．显然S△BCE＝S△FCD．