题目内容
如图所示,带等量异种电荷的两块相互平行的金属板AB、CD长都为L,两板间距为d,其间为匀强电场,当两极板电压U为时,有一质量为m,带电量为q的质子紧靠AB板上的上表面以初速度V射入电场中,设质子运动过程中不会和CD相碰,求:(1)当t=
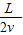 时,质子在竖直方向的位移是多大?
时,质子在竖直方向的位移是多大?(2)当t=
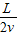 时,突然改变两金属板的电性,且两板间电压为U1,质子恰能沿B端飞出电场,求:电压U1与U的比值是多大?
时,突然改变两金属板的电性,且两板间电压为U1,质子恰能沿B端飞出电场,求:电压U1与U的比值是多大?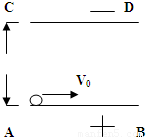
【答案】分析:(1)质子进入电场后,只受电场力,由电场力提供加速度,求出加速度.运动的合成与分解知识,把运动分解为沿电场方向的匀加速直线运动和垂直于电场方向的匀速直线运动.再沿电场方向上,运用匀变速运动的位移公式求解.
(2)求出改变极性时的速度,和改变极性后的加速度,在沿电场的方向上运用匀变速运动的位移公式,列式求解.
解答:解: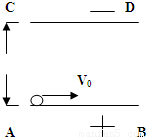 (1)质子进入电场的加速度为
(1)质子进入电场的加速度为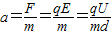
当t=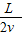 时,质子在竖直方向的位移:
时,质子在竖直方向的位移:
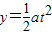 =
=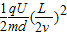 =
=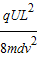
(2)当t=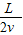 时,质子在竖直方向的速度:
时,质子在竖直方向的速度:
vy=at=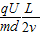 =
=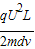
改变两极板的极性后,质子在竖直方向上的加速度:
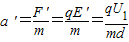
在竖直方向上,由匀变速直线运动公式,得:
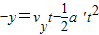
带入以上各数据,有
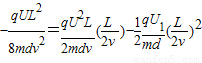
解得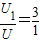
答:(1)当t=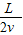 时,质子在竖直方向的位移为
时,质子在竖直方向的位移为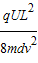 .
.
(2)当t=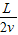 时,突然改变两金属板的电性,且两板间电压为U1,质子恰能沿B端飞出电场,则
时,突然改变两金属板的电性,且两板间电压为U1,质子恰能沿B端飞出电场,则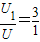 .
.
点评:本题是带点粒子在电场中的运动问题,关键是分析质子的受力情况和运动情况.在偏转电场中质子做类平抛运动,采用运动的分解方法研究.
(2)求出改变极性时的速度,和改变极性后的加速度,在沿电场的方向上运用匀变速运动的位移公式,列式求解.
解答:解:
 (1)质子进入电场的加速度为
(1)质子进入电场的加速度为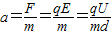
当t=
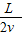 时,质子在竖直方向的位移:
时,质子在竖直方向的位移: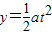 =
=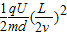 =
=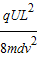
(2)当t=
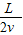 时,质子在竖直方向的速度:
时,质子在竖直方向的速度:vy=at=
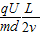 =
=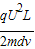
改变两极板的极性后,质子在竖直方向上的加速度:
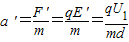
在竖直方向上,由匀变速直线运动公式,得:
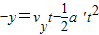
带入以上各数据,有
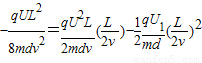
解得
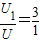
答:(1)当t=
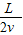 时,质子在竖直方向的位移为
时,质子在竖直方向的位移为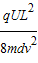 .
.(2)当t=
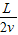 时,突然改变两金属板的电性,且两板间电压为U1,质子恰能沿B端飞出电场,则
时,突然改变两金属板的电性,且两板间电压为U1,质子恰能沿B端飞出电场,则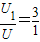 .
.点评:本题是带点粒子在电场中的运动问题,关键是分析质子的受力情况和运动情况.在偏转电场中质子做类平抛运动,采用运动的分解方法研究.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
 如图所示,带等量异种电荷的平行金属板a、b处于匀强磁场中,磁感应强度B垂直纸 面向里,不计重力的带电粒子沿OO′方向从左侧垂直于电磁场入射,从右侧射出a、b板间区域时动能比入射时小.要使粒子射出a、b板间区域时的动能比入射时大,可以( )
如图所示,带等量异种电荷的平行金属板a、b处于匀强磁场中,磁感应强度B垂直纸 面向里,不计重力的带电粒子沿OO′方向从左侧垂直于电磁场入射,从右侧射出a、b板间区域时动能比入射时小.要使粒子射出a、b板间区域时的动能比入射时大,可以( )| A、适当增大金属板间的电压 | B、适当增大金属板间的距离 | C、适当减小金属板间的磁感应强度 | D、使带电粒子的电性相反 |
 (2009?安庆三模)如图所示,带等量异种电荷的两平行金属板竖直放置(M板带正电,N板带负电),板间距为d=80cm,板长为L,板间电压为U=100V.两极板上边缘连线的中点处有一用水平轻质绝缘细线拴接的完全相同的小球A和B组成的装置Q,Q处于静止状态,该装置中两球之间有一处于压缩状态的绝缘轻质小弹簧(球与弹簧不拴接),左边A球带正电,电荷量为q=4×10-5C,右边B球不带电,两球质量均为m=1.0×10-3kg.某时刻,装置Q中细线突然断裂,A、B两球立即同时获得大小相等、方向相反的速度 (弹簧恢复原长).若A、B之间弹簧被压缩时所具有的弹性势能为1.0×10-3J,小球A、B均可视为质点,Q装置中弹簧的长度不计,小球带电不影响板间匀强电场,不计空气阻力,取g=l0m/s2.求:
(2009?安庆三模)如图所示,带等量异种电荷的两平行金属板竖直放置(M板带正电,N板带负电),板间距为d=80cm,板长为L,板间电压为U=100V.两极板上边缘连线的中点处有一用水平轻质绝缘细线拴接的完全相同的小球A和B组成的装置Q,Q处于静止状态,该装置中两球之间有一处于压缩状态的绝缘轻质小弹簧(球与弹簧不拴接),左边A球带正电,电荷量为q=4×10-5C,右边B球不带电,两球质量均为m=1.0×10-3kg.某时刻,装置Q中细线突然断裂,A、B两球立即同时获得大小相等、方向相反的速度 (弹簧恢复原长).若A、B之间弹簧被压缩时所具有的弹性势能为1.0×10-3J,小球A、B均可视为质点,Q装置中弹簧的长度不计,小球带电不影响板间匀强电场,不计空气阻力,取g=l0m/s2.求: (2011?浙江模拟)如图所示,带等量异种电荷,质量分别为m1和m2的两个小球A、B,通过绝缘轻弹簧相连接,置于绝缘光滑的水平面上.当突然加一水平向右的匀强电场后,两小球A、B将由静止开始运动,在以后的运动过程中,对两个小球和弹簧组成的系统(设整个过程中不考虑电荷间库仑力的作用且弹簧不超过弹性限度),以下说法正确的是( )
(2011?浙江模拟)如图所示,带等量异种电荷,质量分别为m1和m2的两个小球A、B,通过绝缘轻弹簧相连接,置于绝缘光滑的水平面上.当突然加一水平向右的匀强电场后,两小球A、B将由静止开始运动,在以后的运动过程中,对两个小球和弹簧组成的系统(设整个过程中不考虑电荷间库仑力的作用且弹簧不超过弹性限度),以下说法正确的是( ) 如图所示,带等量异种电荷的两个相同金属小球A、B(可视为点电荷),相隔一定距离,两球之间的相互吸引力的大小是F.今让第三个相同的不带电金属小球C先后与A、B两球接触后移开,这时A、B两球之间的相互作用力为( )
如图所示,带等量异种电荷的两个相同金属小球A、B(可视为点电荷),相隔一定距离,两球之间的相互吸引力的大小是F.今让第三个相同的不带电金属小球C先后与A、B两球接触后移开,这时A、B两球之间的相互作用力为( ) 如图所示,带等量异种电荷的平行板金属板间有 a、b两点,a 点距A板的距离与 b 点距B板的距离均为 1cm,将一个带电荷量 为0.8×10-4C的正点电荷由 a 点移到 b 点,电场力做了2.0×10-4J的功.若该电荷所受的电场力为 0.01N,则平行板金属板间的距离为
如图所示,带等量异种电荷的平行板金属板间有 a、b两点,a 点距A板的距离与 b 点距B板的距离均为 1cm,将一个带电荷量 为0.8×10-4C的正点电荷由 a 点移到 b 点,电场力做了2.0×10-4J的功.若该电荷所受的电场力为 0.01N,则平行板金属板间的距离为