题目内容
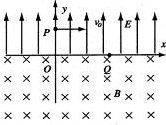
如图所示,边长为L的正方形PQMN区域内(含边界)有垂直于纸面向外的匀强磁场,左侧有水平向右的匀强电场,场强大小为E.质量为m、电荷量为q的带正电粒子从O点由静止开始释放,OPQ三点在同一水平直线上,OP=L,带电粒子从边界NM上的O′点离开磁场,O′与N点距离为
,则磁场磁感应强度的可能数值为(不计带电粒子重力)( )

| L |
| 3 |
A.
| B.3
| C.
| D.2
|

若粒子在匀强磁场中做匀速圆周运动的半径为r1,且r1<L<2r1,
由几何关系得:(L-r1)2+(
)2=r12
解得:r1=
L
由qvB1=m
解得:B1=
同理,若2r2<L<4r2,(L-3r2)2+(
)2=r22
解得:r2=
,B2=3
,
或r′2=
,B′2=
故选:ABC.
由几何关系得:(L-r1)2+(
| L |
| 3 |
解得:r1=
| 5 |
| 9 |
由qvB1=m
| v2 |
| r1 |
解得:B1=
| 9 |
| 5 |
|
同理,若2r2<L<4r2,(L-3r2)2+(
| L |
| 3 |
解得:r2=
| L |
| 3 |
|
或r′2=
| 5L |
| 12 |
| 12 |
| 5 |
|
故选:ABC.

练习册系列答案
相关题目