题目内容
7.如图所示是一个周期性变化的方波电压,其变化周期是T,电压的大小是U.把这个电压加在一对平行金属板上,两板间就形成的电场可视为匀强电场.在两板正中间各有一个小孔A和B.质量为m、带电量为q的粒子从孔A进入平行板之间,重力和初速度可忽略不计,在电场力的作用下,粒子可以从孔B射出.当t=0时有一个上述粒子恰好从孔A进入,从静止开始加速,经过T时间恰好从孔B飞出.
(1)经过$\frac{T}{2}$该粒子的速度是多少?
(2)两板之间的距离d是多大?
(3)如果该粒子是在$\frac{T}{6}$时刻从孔A进入的,则在其出发后第一个周期的时间内粒子通过的位移是多少?
分析 (1)粒子从t=0时刻进入电场,先匀加速运动后匀减速运动,由动能定理求经过$\frac{T}{2}$时粒子的速度.
(2)由于粒子通过电场的时间为T,根据运动过程的对称性知道前、后半个周期内粒子通过的位移相等,由牛顿第二定律和运动学公式结合求解d.
(3)如果该粒子是在$\frac{T}{6}$时刻从孔A进入电场,作出v-t图象,分段求出位移,再得到总位移.
解答 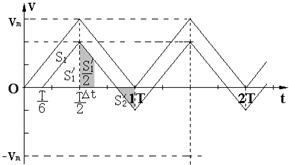 解:(1)由动能定理得$\frac{U}{2}q=\frac{1}{2}m{v^2}$,可得经过$\frac{T}{2}$该粒子的速度为:$v=\sqrt{\frac{Uq}{m}}$
解:(1)由动能定理得$\frac{U}{2}q=\frac{1}{2}m{v^2}$,可得经过$\frac{T}{2}$该粒子的速度为:$v=\sqrt{\frac{Uq}{m}}$
(2)在前、后半个周期内粒子的位移为:${s}_{\frac{T}{2}}$=$\frac{1}{2}•$$\frac{qU}{md}(\frac{T}{2})^{2}$=$\frac{d}{2}$
得:$d=\sqrt{\frac{{qU{T^2}}}{4m}}=\frac{T}{2}\sqrt{\frac{qU}{m}}$
(3)该粒子在$\frac{T}{6}$时刻从孔A进入,作出v-t图象,
设进入电场后刚开始$\frac{1}{3}$T内粒子的位移s1′,则有:
$s_1^/=\frac{1}{2}•\frac{qU}{md}•{({\frac{T}{3}})^2}=\frac{{qU{T^2}}}{18md}$=$\frac{T}{9}\sqrt{\frac{qU}{m}}$
设进入电场后刚开始2T/3内粒子的位移为:
s2′$s_2^/=\frac{1}{2}•\frac{qU}{md}•{({\frac{T}{6}})^2}=\frac{{qU{T^2}}}{72md}$=$\frac{T}{36}\sqrt{\frac{qU}{m}}$
sT′=2s1′-2s2′=2×($\frac{{qU{T^2}}}{18md}$-$\frac{{qU{T^2}}}{72md}$)=$\frac{{qU{T^2}}}{12md}$=$\frac{T}{6}\sqrt{\frac{qU}{m}}$
答:(1)经过$\frac{T}{2}$该粒子的速度是$\sqrt{\frac{Uq}{m}}$.
(2)两板之间的距离d是$\frac{T}{2}\sqrt{\frac{qU}{m}}$.
(3)如果该粒子是在$\frac{T}{6}$时刻从孔A进入的,则在其出发后第一个周期的时间内粒子通过的位移是$\frac{T}{6}\sqrt{\frac{qU}{m}}$.
点评 本题中粒子在周期性变化的电场中运动,关键是明确粒子的受力情况和运动规律,然后结合牛顿第二定律和运动学公式列式求解,可通过v-t图象分析粒子的运动情况.

 如图所示,匀强磁场磁感应强度为B,方向垂直纸面向里.长为L,电阻为R0的金属棒cd在宽为L的导轨上向右滑行,速度为V.已知R1=R2=R0,其余电阻不计,则开关断开和闭合时,M、N两点电势差下列说法正确的是( )
如图所示,匀强磁场磁感应强度为B,方向垂直纸面向里.长为L,电阻为R0的金属棒cd在宽为L的导轨上向右滑行,速度为V.已知R1=R2=R0,其余电阻不计,则开关断开和闭合时,M、N两点电势差下列说法正确的是( )| A. | 断开时,UMN=0;闭合时UMN≠0 | B. | 断开和闭合时,UMN≠0 | ||
| C. | 断开和闭合时MN电势差之比为3:2 | D. | 断开和闭合时MN电势差之比为3:1 |
 如图所示,有一固定的且内壁光滑的半球面,球心为O,最低点为C,在其内壁上有两个质量均为m的小球(可视为质点)A和B,在两个高度不同的水平面内做匀速圆周运动,A球的轨迹平面高于B球的轨迹平面,A、B两球与O点的连线与竖直线OC间的夹角分别为α=53°和β=37°,以最低点C所在的水平面为重力势能的参考平面,则(sin37°=0.6,cos37°=0.8)( )
如图所示,有一固定的且内壁光滑的半球面,球心为O,最低点为C,在其内壁上有两个质量均为m的小球(可视为质点)A和B,在两个高度不同的水平面内做匀速圆周运动,A球的轨迹平面高于B球的轨迹平面,A、B两球与O点的连线与竖直线OC间的夹角分别为α=53°和β=37°,以最低点C所在的水平面为重力势能的参考平面,则(sin37°=0.6,cos37°=0.8)( )| A. | A、B两球所受弹力的大小之比为3:4 | B. | A、B两球运动的周期之比为4:3 | ||
| C. | A、B两球的动能之比为16:9 | D. | A、B两球的重力势能之比为2:1 |
 如图所示,半径为尺的一圆柱形匀强磁场区域的横截面,磁感应强度大小为B,方向垂直于纸面向外,磁场外有一粒子源,能沿一直线发射速度大小不等的在一范围内的同种带电粒子,带电粒子的质量为m,电荷量为q(q>0),不计重力.现粒子以沿正对co中点且垂直于co方向射入磁场区域,发现带电粒子恰能能从bd之间飞出磁场.则( )
如图所示,半径为尺的一圆柱形匀强磁场区域的横截面,磁感应强度大小为B,方向垂直于纸面向外,磁场外有一粒子源,能沿一直线发射速度大小不等的在一范围内的同种带电粒子,带电粒子的质量为m,电荷量为q(q>0),不计重力.现粒子以沿正对co中点且垂直于co方向射入磁场区域,发现带电粒子恰能能从bd之间飞出磁场.则( )| A. | 从b点飞出的带电粒子的速度最大 | B. | 从d点飞出的带电粒子的速度最小 | ||
| C. | 从d点飞出的带电粒子的时间最长 | D. | 从b点飞出的带电粒子的时间最短 |
 如图甲所示,质量为m=2kg的物块沿水平面做直线运动,在拉力作用下的速度图线如图乙中a线所示,撤去拉力后继续运动的图线如图b所示,取重力加速度g=10m/s2,求:
如图甲所示,质量为m=2kg的物块沿水平面做直线运动,在拉力作用下的速度图线如图乙中a线所示,撤去拉力后继续运动的图线如图b所示,取重力加速度g=10m/s2,求: 如图所示,在平面直角坐标系xOy所在的平面内,有垂直于该平面向外的匀强磁场,磁感应强度为B.在xOy平面内,从坐标原点O沿着与x轴正方向成θ=60°角及x轴正方向先后发射电荷量均为+q、质量均为m、速度大小均为v的两个带电粒子.不计粒子的重力和粒子间的相互作用力.两粒子的运动轨迹除O点之外还有一个交点.
如图所示,在平面直角坐标系xOy所在的平面内,有垂直于该平面向外的匀强磁场,磁感应强度为B.在xOy平面内,从坐标原点O沿着与x轴正方向成θ=60°角及x轴正方向先后发射电荷量均为+q、质量均为m、速度大小均为v的两个带电粒子.不计粒子的重力和粒子间的相互作用力.两粒子的运动轨迹除O点之外还有一个交点. 如图所示,空间存在一个半径为R0的圆形匀强磁场区域,磁场的方向垂直于纸面向里,磁感应强度的大小为B.有一个粒子源在纸面内沿各个方向以一定速率发射大量粒子,粒子的质量为m、电荷量为+q.将粒子源置于圆心,则所有粒子刚好都不离开磁场.(不考虑粒子的重力及粒子之间的相互作用)
如图所示,空间存在一个半径为R0的圆形匀强磁场区域,磁场的方向垂直于纸面向里,磁感应强度的大小为B.有一个粒子源在纸面内沿各个方向以一定速率发射大量粒子,粒子的质量为m、电荷量为+q.将粒子源置于圆心,则所有粒子刚好都不离开磁场.(不考虑粒子的重力及粒子之间的相互作用)