题目内容
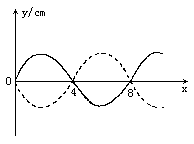
如图所示为一列沿x轴向右传播的简谐横波在某时刻的波动图像,已知此波的传播速度大小为v=2m/s.试画出该时刻5s前及5s后的波动图像.
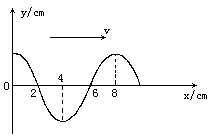
答案:
解析:
提示:
解析:
|
方法一 (特殊质点振动法):因为波速v=2m/s,从图得λ=8m,所以T=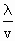 =4s,又因为此波向右传播,故平衡位置坐标为2m、6m的两个特殊质点的初始振动方向分别为沿y轴正向与沿y轴负向,经过5s(1 =4s,又因为此波向右传播,故平衡位置坐标为2m、6m的两个特殊质点的初始振动方向分别为沿y轴正向与沿y轴负向,经过5s(1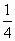 T),这两个质点分别位于正向最大位移与负向最大位移,由此得出5s后的波形如下图中实线所示,同样的道理,只需设想各质点逆向振动1 T),这两个质点分别位于正向最大位移与负向最大位移,由此得出5s后的波形如下图中实线所示,同样的道理,只需设想各质点逆向振动1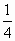 T,即得5s前的波形图像如图中虚线所示. T,即得5s前的波形图像如图中虚线所示.
方法二 (波形平移法):因为波速v=2m/s,所以由Δx=vΔt可得Δx=10m,注意到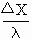 去整后为 去整后为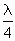 ,故将整个波形向右平移 ,故将整个波形向右平移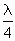 ,即为5s后的波动图像.而将整个波形向左平移 ,即为5s后的波动图像.而将整个波形向左平移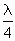 ,即5s前的波动图像. ,即5s前的波动图像.
【评析】此类问题中要计算出Δ t相当于多少个周期.由于波动图像的周期性,可以去整留零,即只画出不足一个周期的部分. |
提示:
|
【分析】画 5s前和5s后的波动图象即要得到5s前和5s后各质点在空间上的分布情况. |

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 如图所示为一列沿x轴正方向传播的简谐横波在t=0时的波形.当R点在t=0时的振动状态传到S点时,PR范围内(含P、R)有一些质点正在向y轴负方面运动,这些质点的x坐标取值范围是
如图所示为一列沿x轴正方向传播的简谐横波在t=0时的波形.当R点在t=0时的振动状态传到S点时,PR范围内(含P、R)有一些质点正在向y轴负方面运动,这些质点的x坐标取值范围是 如图所示为一列沿x轴正方向传播的简谐横波在某时刻的波形图.此时( )
如图所示为一列沿x轴正方向传播的简谐横波在某时刻的波形图.此时( ) 如图所示为一列沿x轴传播的简谐横波某时刻的图象,已知从该时刻起,图中质点A经时间0.1秒第一次经过平衡位置,而图中的质点B第一次经过平衡位置所需的时间大于0.1秒,则下列说法中正确的是( )
如图所示为一列沿x轴传播的简谐横波某时刻的图象,已知从该时刻起,图中质点A经时间0.1秒第一次经过平衡位置,而图中的质点B第一次经过平衡位置所需的时间大于0.1秒,则下列说法中正确的是( ) 如图所示为一列沿x轴正方向传播的简谐横波在t=0时刻的波形图象(图中仅画出0~12m范围内的波形).经过△t=1.2s的时间,恰好第三次重复出现图示的波形.根据提供的信息,下列判断中正确的( )
如图所示为一列沿x轴正方向传播的简谐横波在t=0时刻的波形图象(图中仅画出0~12m范围内的波形).经过△t=1.2s的时间,恰好第三次重复出现图示的波形.根据提供的信息,下列判断中正确的( ) (2009?泉州二模)如图所示为一列沿x轴传播的简谐横波在t时刻的波形图,下列关于a、b两质点的说法中正确的是( )
(2009?泉州二模)如图所示为一列沿x轴传播的简谐横波在t时刻的波形图,下列关于a、b两质点的说法中正确的是( )