题目内容
环形对撞机是研究高能粒子的重要装置.初速为零的带电粒子经电压为U的电场加速后注入对撞机的高真空圆环形状的空腔内,在匀强磁场中,做半径恒定的圆周运动.关于带电粒子的比荷q/m,加速电压U和磁感应强度B以及粒子运动的周期T的关系,下列说法中正确的是( )A.对于给定的加速电压,带电粒子的比荷q/m越大,磁感应强度B越小
B.对于给定的加速电压,带电粒子的比荷q/m越大,磁感应强度B越大
C.对于给定的带电粒子,加速电压U越大,粒子运动的周期T越小
D.对于给定的带电粒子,不管加速电压U多大,粒子运动的周期T都不变
【答案】分析:带电粒子在电场中被加速后,进入匀强磁场后做匀速圆周运动.由题知,带电粒子圆周运动的半径都相同,则由半径公式与粒子在电场中加速公式: mv2=qU,研究粒子的比荷和磁感应强度、周期的关系.
mv2=qU,研究粒子的比荷和磁感应强度、周期的关系.
解答:解:带电粒子在匀强磁场中做匀速圆周运动,由洛伦兹力提供向心力可知:Bqv=m 得R=
得R= (1)
(1)
而粒子在电场中被加速,则有: mv2=qU (2)
mv2=qU (2)
将(1)(2)两式联立可得:R= ,
,
带电粒子运行的周期T= .
.
A、B对于给定的加速电压,由于半径R相同,由上式得知,带电粒子的比荷 越大,磁感应强度B越小.故A正确,B错误.
越大,磁感应强度B越小.故A正确,B错误.
C、D对于给定的带电粒子,比荷 一定,磁感应强度B一定,则粒子运动周期一定,与加速电压无关.故C错误,D正确.
一定,磁感应强度B一定,则粒子运动周期一定,与加速电压无关.故C错误,D正确.
故选AD
点评:本题通过洛伦兹力提供向心力来导出半径公式与周期公式,再用动能定理得出粒子在电场中的加速公式,从而可推导出加速电压、磁感应强度、粒子的比荷及半径的关系.最终由控制变量来研究其它各量之间的具体关系.
 mv2=qU,研究粒子的比荷和磁感应强度、周期的关系.
mv2=qU,研究粒子的比荷和磁感应强度、周期的关系.解答:解:带电粒子在匀强磁场中做匀速圆周运动,由洛伦兹力提供向心力可知:Bqv=m
 得R=
得R= (1)
(1)而粒子在电场中被加速,则有:
 mv2=qU (2)
mv2=qU (2)将(1)(2)两式联立可得:R=
 ,
,带电粒子运行的周期T=
 .
.A、B对于给定的加速电压,由于半径R相同,由上式得知,带电粒子的比荷
 越大,磁感应强度B越小.故A正确,B错误.
越大,磁感应强度B越小.故A正确,B错误.C、D对于给定的带电粒子,比荷
 一定,磁感应强度B一定,则粒子运动周期一定,与加速电压无关.故C错误,D正确.
一定,磁感应强度B一定,则粒子运动周期一定,与加速电压无关.故C错误,D正确.故选AD
点评:本题通过洛伦兹力提供向心力来导出半径公式与周期公式,再用动能定理得出粒子在电场中的加速公式,从而可推导出加速电压、磁感应强度、粒子的比荷及半径的关系.最终由控制变量来研究其它各量之间的具体关系.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 环形对撞机是研究高能粒子的重要装置,如图所示,正、负离子由静止经过电压为U的直线加速器后,沿圆环切线方向注入对撞机的真空环状空腔内,空腔内存在着与圆环水平垂直的匀强磁场,磁感应强度大小为B,两种带电粒子将被局限在环状空腔内,只在洛伦兹力作用下,沿相反方向做半径相等的匀速圆周运动,从而在碰撞区迎面相撞,为维持带电粒子在环状空腔中的匀速圆周运动,下列说法正确的是( )
环形对撞机是研究高能粒子的重要装置,如图所示,正、负离子由静止经过电压为U的直线加速器后,沿圆环切线方向注入对撞机的真空环状空腔内,空腔内存在着与圆环水平垂直的匀强磁场,磁感应强度大小为B,两种带电粒子将被局限在环状空腔内,只在洛伦兹力作用下,沿相反方向做半径相等的匀速圆周运动,从而在碰撞区迎面相撞,为维持带电粒子在环状空腔中的匀速圆周运动,下列说法正确的是( )| A、对于给定的带电粒子,加速电压U越大,粒子的运动周期越大 | ||
| B、对于给定的带电粒子,不管加速电压U如何变化,粒子的运动周期都保持不变 | ||
C、对于给定的加速电压,带点粒子的比荷
| ||
D、对于给定的加速电压,带点粒子的比荷
|
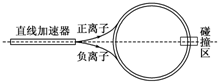 环形对撞机是研究高能离子的重要装置,如图所示正、负离子由静止经过电压为U的直线加速器加速后,沿圆环切线方向注入对撞机的真空环状空腔内,空腔内存在着与圆环平面垂直的匀强磁场,磁感应强度大小为B.(两种带电粒子将被局限在环状空腔内,沿相反方向做半径相等的匀速圆周运动,从而在碰撞区迎面相撞)为维持带电粒子在环状空腔中的匀速圆周运动,下列说法正确的是( )
环形对撞机是研究高能离子的重要装置,如图所示正、负离子由静止经过电压为U的直线加速器加速后,沿圆环切线方向注入对撞机的真空环状空腔内,空腔内存在着与圆环平面垂直的匀强磁场,磁感应强度大小为B.(两种带电粒子将被局限在环状空腔内,沿相反方向做半径相等的匀速圆周运动,从而在碰撞区迎面相撞)为维持带电粒子在环状空腔中的匀速圆周运动,下列说法正确的是( )A、对于给定的加速电压,带电粒子的比荷
| ||
B、对于给定的加速电压,带电粒子的比荷
| ||
| C、对于给定的带电粒子,不管加速电压U多大,粒子运动的周期都不变 | ||
| D、对于给定的带电粒子,加速电压U越大,粒子运动的周期越小 |
 (2010?邵阳模拟)环形对撞机是研究高能粒子的重要装置.正、负离子由静止经过电压为U的直线加速器加速后,沿圆环切线方向注人对撞机的真空环状空腔内,空腔内存在着与圆环平面垂直的匀强磁场,磁感应强度大小为B,两种带电粒子将被局限在环状空腔内,沿相反方向做半径相等的匀速圆周运动,从而在碰撞区迎面相撞,为维持带电粒子在环状空腔中的匀速圆周运动,下列说法正确的是( )
(2010?邵阳模拟)环形对撞机是研究高能粒子的重要装置.正、负离子由静止经过电压为U的直线加速器加速后,沿圆环切线方向注人对撞机的真空环状空腔内,空腔内存在着与圆环平面垂直的匀强磁场,磁感应强度大小为B,两种带电粒子将被局限在环状空腔内,沿相反方向做半径相等的匀速圆周运动,从而在碰撞区迎面相撞,为维持带电粒子在环状空腔中的匀速圆周运动,下列说法正确的是( )