题目内容
11. 如图所示,一小车由半径为R的四分之一光滑圆弧AB和粗糙的足够长的水平部分BC组成,两部分相切于B点,小车质量为M,静止在光滑的水平地面上,一物块质量为m=$\frac{1}{2}$M,从小车上A点处由静止释放,与BC部分动摩擦因数为μ,重力加速度为g,求:
如图所示,一小车由半径为R的四分之一光滑圆弧AB和粗糙的足够长的水平部分BC组成,两部分相切于B点,小车质量为M,静止在光滑的水平地面上,一物块质量为m=$\frac{1}{2}$M,从小车上A点处由静止释放,与BC部分动摩擦因数为μ,重力加速度为g,求:(1)运动过程中,小车的最大速度;
(2)小物块在BC部分滑过的最大距离.
分析 (1)物块到达B点时小车受到最大,物块与小车组成的系统在水平方向动量守恒,应用动量守恒定律与机械能守恒定律可以求出小车的最大速度.
(2)应用能量守恒定律可以求出物块滑行的距离.
解答 解:(1)物块到达B点时小车的速度最大,物块与小车组成的系统在水平方向动量守恒,
以向右为正方向,由动量守恒定律得:mv-Mv′=0,
系统机械能守恒,由机械能守恒定律得:mgR=$\frac{1}{2}$mv2+$\frac{1}{2}$Mv′2,
解得:v′=$\sqrt{\frac{gR}{3}}$;
(2)对系统,由能量守恒定律得:μmgs=mgR,解得:x=$\frac{R}{μ}$;
答:(1)运动过程中,小车的最大速度为$\sqrt{\frac{gR}{3}}$;
(2)小物块在BC部分滑过的最大距离为$\frac{R}{μ}$.
点评 小车与物块组成的系统在水平方向所受合外力为零,系统在水平方向动量守恒,物块在BC上运动过程克服摩擦力做功,把系统的机械能转化为内能,分析清楚物体运动过程,应用动量守恒定律、机械能守恒定律与能量守恒定律可以正确解题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
1.物理关系式不仅反映了物理量之间的数量关系,也确定了物理量之间的单位关系.现有物理量单位:m(米)、s(秒)、J(焦)、W(瓦)、C(库)、A(安)、Ω(欧)和T(特),由它们组合成的单位与电压单位V(伏)等效的是( )
| A. | J/A | B. | W/Ω | C. | T•m2/s | D. | T•A•m |
2. 如图所示,某理想变压器的原副线圈的匝数均可调节,原线圈两端接电压为一最大值不变的正弦交流电,在其他条件不变的情况下,为了使变压器输入功率增大,可使( )
如图所示,某理想变压器的原副线圈的匝数均可调节,原线圈两端接电压为一最大值不变的正弦交流电,在其他条件不变的情况下,为了使变压器输入功率增大,可使( )
 如图所示,某理想变压器的原副线圈的匝数均可调节,原线圈两端接电压为一最大值不变的正弦交流电,在其他条件不变的情况下,为了使变压器输入功率增大,可使( )
如图所示,某理想变压器的原副线圈的匝数均可调节,原线圈两端接电压为一最大值不变的正弦交流电,在其他条件不变的情况下,为了使变压器输入功率增大,可使( )| A. | 原线圈匝数n1增加 | B. | 副线圈匝数n2增加 | ||
| C. | 负载电阻R的阻值减小 | D. | 负载电阻R的阻值增大 |
19.下列说法正确的是( )
| A. | 康普顿效应说明光具有粒子性 | |
| B. | ${\;}_{92}^{235}$U的半衰期约为7亿年,随地球环境的变化,半衰期可能变短 | |
| C. | 在α射线、β射线、γ射线中,β射线是高速电子流,电离作用最强 | |
| D. | -束光照射到金属上,从金属表面逸出光电子,仅增加光的强度,光电子最大初动能不变 | |
| E. | 氢原子的核外电子由较高能级跃迁到较低能级时,要释放一定频率的光子,同时电子的动能增加,电势能减小 |
16.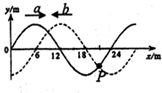 两列振幅为2cm、波长24cm和波速12m/s简谐横波a和b,分别沿x轴正方向和负方向传播.在t=0时刻的部分波形图如图所示,则( )
两列振幅为2cm、波长24cm和波速12m/s简谐横波a和b,分别沿x轴正方向和负方向传播.在t=0时刻的部分波形图如图所示,则( )
 两列振幅为2cm、波长24cm和波速12m/s简谐横波a和b,分别沿x轴正方向和负方向传播.在t=0时刻的部分波形图如图所示,则( )
两列振幅为2cm、波长24cm和波速12m/s简谐横波a和b,分别沿x轴正方向和负方向传播.在t=0时刻的部分波形图如图所示,则( )| A. | 图中x=15m处的质点是加强点 | |
| B. | 图中x=21m处的P质点经时间t=0.75出现速度最大值 | |
| C. | 此两列波相遇不能发生干涉现象 | |
| D. | 该两波如要发生明显的衍射现象,所遇到的障碍物的尺寸一般不大于2cm |
3.下列说法中正确的是( )
| A. | 计算交流电的有效值时运用了等效替代方法 | |
| B. | 牛顿发现了万有引力定律,并计算出太阳与地球间引力的大小 | |
| C. | 伽利略在证明自由落体运动时匀变速直线运动时,采用了理想实验法 | |
| D. | 安培首先发现了电流的磁效应,并提出了判断电流周围磁场方向的方法-安培定则 |

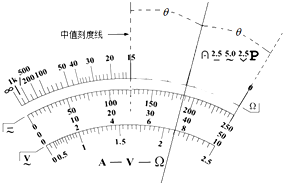 现有一多用电表,其欧姆挡的“0”刻度线与中值刻度线之间的刻度模糊,若用“×100”的欧姆挡,经调零后,规范测量某一待测电阻R,指针所指的位置与“0”刻度线和中值刻度线间的夹角相等,如图所示,则该待测电阻R=500Ω.
现有一多用电表,其欧姆挡的“0”刻度线与中值刻度线之间的刻度模糊,若用“×100”的欧姆挡,经调零后,规范测量某一待测电阻R,指针所指的位置与“0”刻度线和中值刻度线间的夹角相等,如图所示,则该待测电阻R=500Ω.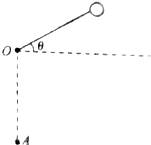 如图所示,摆球的质量为m,从偏离水平方向θ=30°的位置由静止释放,求:
如图所示,摆球的质量为m,从偏离水平方向θ=30°的位置由静止释放,求: