题目内容
(13分)一电子通过电压为4500V的加速电场加速后获得速度,沿垂直电场线方向进入场强为1.5×105V/m的匀强电场中。电子从进入电场的一点c点到达电场中另一点d点时,电子的速度方向刚好与场强方向成120o的夹角,如图所示。则:

(1)c、d两点沿场强方向的距离为多少?
(2)c、d两点的电势差为多少?
【答案】
0.01m -1500V
【解析】(1)假设电子质量m,带电量-e,加速电场电压U=4500V,进入偏转电场c时速度v0
由题意电子经过加速电场,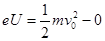 ①
①
电子经偏转电场到d点,沿电场力方向速度分量vy=v0tan30° ②
沿电场力方向,电子以加速度a,做匀加速直线运动,则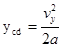 ③
③
由牛顿第二定律,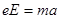 ④
④
联立①②③④式,带入数据解得ycd=0.01m
(2)设cd间电压为Ucd
由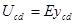 ,带入数据得Ucd=1500V
,带入数据得Ucd=1500V
根据电场分布,可知c点电势低于d点电势,所以cd间电势差为-1500V.
思路分析:根据动能定理求出经过加速之后的速度,利用速度的矢量求出沿电场方向速度,根据匀加速求出的偏转位移;利用电场力做功公式计算C、D间的电势差。
试题点评:考查电场力做功和带电粒子在电场中的偏转

练习册系列答案
相关题目

 选做题:请从A、B和C三小题中选定两小题作答,并在答题卡上把所选题目对应字母后的方框涂满涂黑.如都作答,则按A、B两小题评分.
选做题:请从A、B和C三小题中选定两小题作答,并在答题卡上把所选题目对应字母后的方框涂满涂黑.如都作答,则按A、B两小题评分.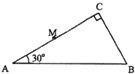
 ;
; .在此截面所在的平面内,一条光线以45°的入射角从AC边的中点M射入棱镜,求射出点的位置(不考虑光线沿原来路返回的情况).
.在此截面所在的平面内,一条光线以45°的入射角从AC边的中点M射入棱镜,求射出点的位置(不考虑光线沿原来路返回的情况).

