题目内容
14.在“探究加速度与力、质量的关系”的实验中:(1)对于本实验,以下说法中正确的是CD
A.砂和桶的总质量要远大于小车的总质量
B.每次改变小车质量后,需要重新平衡摩擦力
C.实验中也可不测加速度的具体数值,只要测出不同情况下加速度的比值就行了
D.若要验证“加速度与力的平方成正比”这一猜想,在作图线时最好以F2为横坐标
(2)某同学在接通电源进行实验之前,将 实验器材组装如图1所示,下列对此同学操作的判断正确的是BCD
A.打点计时器不应固定在长木板的最右端,而应固定在靠近定滑轮的那端
B.打点计时器不应使用干电池,而应使用交流电源
C.不应将长木板水平放置,而应在右端垫起合适的高度,平衡摩擦力
D.小车初始位置不应离打点计时器太远,而应靠近打点计时器放置
(3)改正实验装置后,该同学顺利地完成了实验.在实验中保持拉力不变,得到了小车加速度随质量变化的一组数据,如表所示:
| 实验次数 | 加速度 a/m•s-2 | 小车与砝码总质量 m/kg | 小车与砝码总质量的倒数 m-1/kg-1 |
| 1 | 0.32 | 0.20 | 5.0 |
| 2 | 0.25 | 0.25 | 4.0 |
| 3 | 0.21 | 0.30 | 3.3 |
| 4 | 0.18 | 0.35 | 2.9 |
| 5 | 0.16 | 0.40 | 2.5 |
(4)从图线可得出拉力大小为0.062N(结果保留两位有效数字).

(5)保持小车质量不变,改变砂和砂桶质量,某同学根据实验数据作出了加速度a随合力F的变化图线如图3所示.此图中直线发生明显弯曲的原因是随着F的增大,不再满足砂和桶的总质量远小于小车的总质量.
分析 (1)明确实验原理,正确对实验进行数据处理和了解具体操作的含义;
(2)打点计时器应固定在没有定滑轮的一端,打点计时器使用交流了电;实验时应平衡摩擦力;开始时小车应靠近打点计时器.
(3)根据牛顿第二定律可知,加速度和质量成反比,故应该做a-$\frac{1}{m}$图象;采用描点法作图即可.
(4)通过加速度与质量关系的图线的斜率,即可求解拉力大小;
(5)直线发生明显弯曲的原因是砂和桶的总质量没有远小于小车的总质量.
解答 解:(1)A、砂和桶的总质量要远小于小车的总质量,故A错误;
B、每次改变小车质量后,不需要重新平衡摩擦力,因为动摩擦力因数与倾角没变,故B错误;
C、实验中也可不测加速度的具体数值,只要测出不同情况下加速度的比值就行了,故C正确;
D、要验证“加速度与力的平方成正比”这一猜想,在作图线时最好以F的平方为横坐标,故D正确;
所以选:CD.
(2)打点计时器使用的是交流电源,而干电池是直流电源;接通电源前,小车应紧靠打点计时器,而在该图中小车初始位置离打点计时器太远;应在右端垫起合适的高度,平衡摩擦力;
A、打点计时器应固定在长木板的最右端,故A错误;
B、打点计时器不应使用干电池,而应使用交流电源,故B正确;
C、不应将长木板水平放置,而应在右端垫起合适的高度,平衡摩擦力,故C正确;
D、小车初始位置不应离打点计时器太远,而应靠近打点计时器放置,故D正确;
所以选:BCD.
(3)在合外力保持不变时,物体的加速度与物体的质量成反比;
根据表中数据利用描点法可作出加速度与小车质量倒数的关系图象,如图所示;
(4)根据图线的数据,求得,图线的斜率为k=$\frac{0.25}{4}$=0.062,即拉力的大小为0.062N;
(5)图中直线发生明显弯曲的原因是:随着F的增大,不再满足砂和桶的总质量远小于小车的总质量;
故答案为:
(1)C; (2)BCD;(3)如上图;(4)0.061~0.065N;(5)随着F的增大,不再满足砂和桶的总质量远小于小车的总质量
点评 本题考查“探究加速度与力、质量的关系”的实验,解题时要注意明确用图想法处理数据时,要作直线,直线较为形象直观.验证牛顿第二定律实验应采用控制变量法,掌握描点法作图的方法、实验注意事项即可正确解题.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案| A. | 在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫假设法 | |
| B. | 根据速度定义式v=$\frac{△x}{△t}$,当△t非常非常小时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义应用了极限思维法 | |
| C. | 玻璃瓶内装满水,用穿有透明细管的橡皮泥封口.手捏玻璃瓶,细管内液面高度变化,说明玻璃瓶发生形变,该实验采用放大的思想 | |
| D. | 在推导匀变速运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法 | |
| E. | 牛顿提出了万有引力定律,并计算出了太阳和地球之间的引力 |
| A. | ${\;}_{11}^{24}$Na→${\;}_{12}^{24}$Mg+${\;}_{-1}^{0}$e是原子核衰变方程 | |
| B. | ${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{56}^{141}$Ba+${\;}_{36}^{92}$Kr+3${\;}_{0}^{1}$n是原子核人工转变方程 | |
| C. | ${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{8}^{17}$O+${\;}_{1}^{1}$H是原子核聚变方程 | |
| D. | ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n是原子核裂变方程 |
| A. | 加速、减速中的加速度大小之比为a1:a2=2:1 | |
| B. | 加速、减速中的平均速度大小之比为$\overline{{v}_{1}}$:$\overline{{v}_{2}}$=1:1 | |
| C. | 加速、减速中的位移之比s1:s2=2:1 | |
| D. | 加速、减速中的加速度大小之比为a1:a2=1:1 |
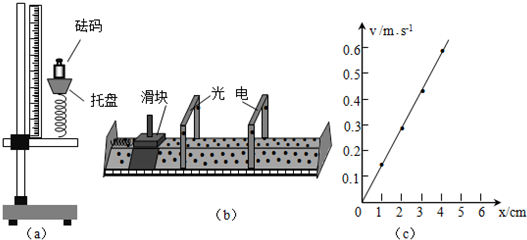
①如图(a),将轻质弹簧下端固定于铁架台,在上端的托盘中依次增加砝码,测得相应的弹簧长度,部分数据如下表,有数据算得劲度系数k=50N/m.(g取10m/s2)
| 砝码质量(g) | 50 | 100 | 150 |
| 弹簧长度(cm) | 8.63 | 7.64 | 6.62 |
③用滑块压缩弹簧,记录弹簧的压缩量x;释放滑块,记录滑块脱离弹簧后的速度v,释放滑块过程中,弹簧的弹性势能转化为滑块的动能.
④重复③中的操作,得到v与x的关系如图(c).有图可知,v与x成正比关系,由上述实验可得结论:对同一根弹簧,弹性势能与弹簧的压缩量的平方成正比.
 如图所示,小车板面上的物体质量为m=8kg,它被一根水平方向上拉伸了的弹簧拉住而静止在小车上,这时弹簧的弹力为6N.现沿水平向右的方向对小车施以作用力,使小车由静止开始运动起来,运动中加速度由零逐渐增大到1m/s2,随即以1m/s2的加速度做匀加速直线运动.以下说法正确的是( )
如图所示,小车板面上的物体质量为m=8kg,它被一根水平方向上拉伸了的弹簧拉住而静止在小车上,这时弹簧的弹力为6N.现沿水平向右的方向对小车施以作用力,使小车由静止开始运动起来,运动中加速度由零逐渐增大到1m/s2,随即以1m/s2的加速度做匀加速直线运动.以下说法正确的是( )| A. | 物体与小车始终保持相对静止,弹簧对物体的作用力始终没有发生变化 | |
| B. | 物体受到的摩擦力一直减小 | |
| C. | 当小车加速度(向右)为0.75 m/s2时,物体不受摩擦力作用 | |
| D. | 如小车以0.5m/s2的加速度向左做匀加速直线运动时,物体受到的摩擦力一定为10 N |
 如图所示,在粗糙水平板上放一个物体,使水平板和物体一起在竖直平面内沿逆时针方向做匀速圆周运动,ab为水平直径,cd为竖直直径,在运动过程中木板始终保持水平,物块相对木板始终静止,则( )
如图所示,在粗糙水平板上放一个物体,使水平板和物体一起在竖直平面内沿逆时针方向做匀速圆周运动,ab为水平直径,cd为竖直直径,在运动过程中木板始终保持水平,物块相对木板始终静止,则( )| A. | 物块始终受到三个力作用 | |
| B. | 从a到b,物体所受的摩擦力先减小后增大 | |
| C. | 从b到a,物块处于超重状态 | |
| D. | 只有在a、b、c、d四点,物块受到合外力才指向圆心 |
 图中实线是一组不知方向的匀强电场的电场线,把2×10-6C的负电荷从A点沿水平方向移到B点,电场力做了2×10-6J的功.A、B两点间距离为2cm,问
图中实线是一组不知方向的匀强电场的电场线,把2×10-6C的负电荷从A点沿水平方向移到B点,电场力做了2×10-6J的功.A、B两点间距离为2cm,问